3.20 周回積分
注意 3.93 (周回積分)
積分路 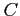 が一周しているとき,
線積分
が一周しているとき,
線積分
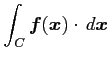 を
を
と表記することがある. これを周回積分とも呼ぶ.
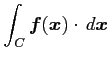 を
を
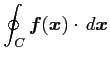 |
と表記することがある. これを周回積分とも呼ぶ.
定義 3.94 (領域の境界)
領域 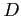 の境界を
の境界を
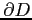 と表記する.
このとき内部が進行方向の左手になるように向きを定める.
(注意)ここで
と表記する.
このとき内部が進行方向の左手になるように向きを定める.
(注意)ここで 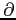 は偏微分の記号とは全く関係ない.
単に記号の形が「ぐるっとまわる」の見えるため.
は偏微分の記号とは全く関係ない.
単に記号の形が「ぐるっとまわる」の見えるため.
例 3.95 (周回積分)
線積分
を計算する. ただし, 積分路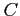 は
は 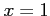 ,
, 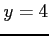 ,
, 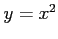 (
(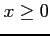 ) で囲まれる領域の境界を
正の向きに回るとする.
積分路を分割すると,
) で囲まれる領域の境界を
正の向きに回るとする.
積分路を分割すると,
と書ける. 線積分は
となる.
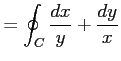 |
を計算する. ただし, 積分路
と書ける. 線積分は
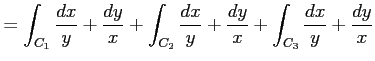 |
||
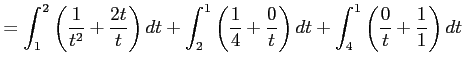 |
||
![$\displaystyle = \int_{1}^{2}\frac{dt}{t^2}+ 2\int_{1}^{2}dt+\frac{1}{4}\int_{2}...
...idth0em depth0.1em\,{-\frac{1}{t}}\,\right]_{1}^{2}+ 2(2-1)+\frac{1-2}{4}+(1-4)$](img2502.png) |
||
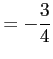 |
となる.
例 3.96 (周回積分)
周回積分
を求める. ただし,積分路は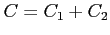 ,
,
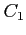 : 中心は原点,半径
: 中心は原点,半径 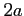 の円を正の向きに一周,
の円を正の向きに一周,
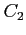 : 中心は原点,半径
: 中心は原点,半径 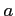 の円を負の向きに一周とする.
積分路は
の円を負の向きに一周とする.
積分路は
と書けるので, 線積分は
と求まる.
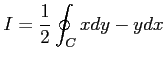 |
を求める. ただし,積分路は
と書けるので, 線積分は
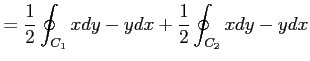 |
||
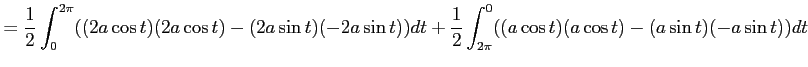 |
||
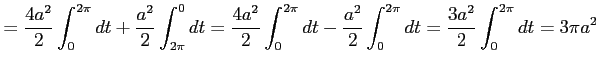 |
と求まる.
平成21年12月2日