2.36 平均値の定理
定理 2.156 (平均値の定理)
関数 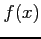 が連続かつ微分可能であるとき,
が連続かつ微分可能であるとき,
をみたす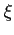 が存在する.
が存在する.
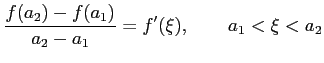 |
をみたす
定理 2.157 (平均値の定理)
関数 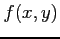 が連続かつ全微分可能であるとき,
が連続かつ全微分可能であるとき,
をみたす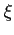 ,
, 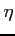 が存在する.
が存在する.
をみたす
問 2.158 (平均値の定理)
次の等式が成り立つことを示せ.
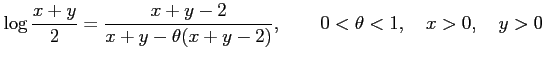 |
平成21年12月2日
2.36 平均値の定理
定理 2.156 (平均値の定理) 関数が連続かつ微分可能であるとき,
をみたすが存在する.
定理 2.157 (平均値の定理) 関数が連続かつ全微分可能であるとき,
をみたす,
が存在する.
問 2.158 (平均値の定理) 次の等式が成り立つことを示せ.
平成21年12月2日