2.20 外積を用いて平面の法線ベクトルを導出
例 2.49 (
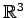 の平面の方程式の具体例)
3 点
の平面の方程式の具体例)
3 点 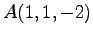 ,
, 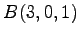 ,
, 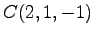 を通る
を通る
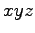 空間内の平面を考える.
法線ベクトルは
空間内の平面を考える.
法線ベクトルは
であり,点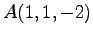 を通るので,
を通るので,
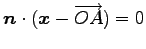 より
平面の方程式
より
平面の方程式
を得る.一般形で書けば
となる.さらに変形して
とする. 平面と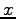 軸,
軸,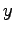 軸,
軸,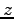 軸の交点はそれぞれ
軸の交点はそれぞれ
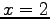 ,
, 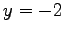 ,
, 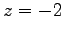 である.
である.
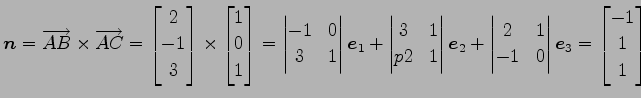 |
であり,点
を得る.一般形で書けば
となる.さらに変形して
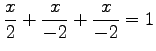 |
とする. 平面と
平成20年4月22日