2.10 ベクトルの直交
定義 2.18 (ベクトルの直交)
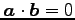 のとき
のとき 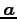 と
と 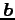 は
直交する(orthogonal)という.
このとき
は
直交する(orthogonal)という.
このとき
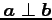 と表記する.
と表記する.
例 2.19 (ベクトルの直交の具体例)
を考える.このとき
が成り立つ.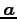 と
と 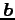 は互いに直交する.
は互いに直交する.
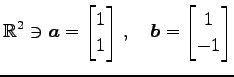 |
(47) |
を考える.このとき
| (48) |
が成り立つ.
平成20年4月22日
2.10 ベクトルの直交
定義 2.18 (ベクトルの直交)のとき
と
は 直交する(orthogonal)という. このとき
と表記する.
例 2.19 (ベクトルの直交の具体例)
(47)
を考える.このとき
(48)
が成り立つ.と
は互いに直交する.
平成20年4月22日