2.3 位置ベクトル
定義 2.6 (位置ベクトル)
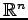 空間内の点
空間内の点
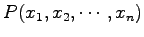 と
原点
と
原点
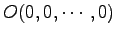 より得られるベクトル
より得られるベクトル
を点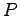 の位置ベクトル(position vector) という.
点
の位置ベクトル(position vector) という.
点 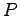 とベトクル
とベトクル 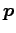 を同一視する.
を同一視する.
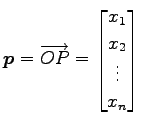 |
(21) |
を点
注意 2.7 (位置ベクトル)
点 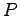 の座標が
の座標が
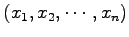 のときは,
のときは,
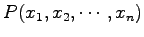 と表記する.
点
と表記する.
点 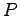 の位置ベクトルが
の位置ベクトルが 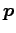 のときは,
のときは,
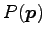 と表記することにする.
と表記することにする.
平成20年4月22日