3.1 多重積分
注意 3.1 (定積分)
1 変数関数 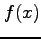 を考える.
区間
を考える.
区間 ![$ [a,b]$](img1937.png) を
を
と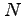 個に分割し,
各小区間の幅を
個に分割し,
各小区間の幅を
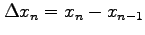 とおく.
このとき,各小区間の矩形の符合付き面積は
とおく.
このとき,各小区間の矩形の符合付き面積は
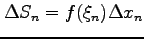 (
(
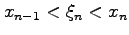 ) であるから,
曲線
) であるから,
曲線 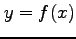 と区間
と区間 ![$ [a,b]$](img1937.png) における符合付きの面積は
における符合付きの面積は
で与えられ,これが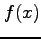 の定積分である.
また,定積分においては区間についても向きがあることに注意する.
の定積分である.
また,定積分においては区間についても向きがあることに注意する.
と
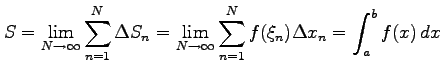 |
で与えられ,これが
注意 3.2 (定積分と区間の長さ)
被積分関数が 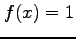 のとき,定積分
のとき,定積分
は区間![$ I=[a,b]$](img1946.png) の長さを表す.
の長さを表す.
![$\displaystyle \int_{a}^{b}dx= \left[\vrule height1.5em width0em depth0.1em\,{x}\,\right]_{a}^{b}=b-a$](img1945.png) |
は区間
![\includegraphics[width=0.5\textwidth]{area.eps}](img1947.png) |
![\includegraphics[width=0.5\textwidth]{length.eps}](img1948.png) |
定義 3.3 (2 重積分)
長方形領域
を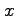 軸方向に
軸方向に 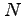 分割し,
分割し,
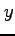 軸方向に
軸方向に 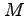 分割し,
分割し,
とする. 各小領域
の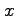 方向,
方向,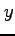 方向の幅を
方向の幅を
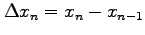 ,
,
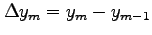 とおくと,
小領域
とおくと,
小領域 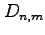 の面積は
の面積は
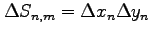 であり,
曲面
であり,
曲面 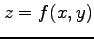 と
と 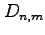 ではさまれた領域の体積は
ではさまれた領域の体積は
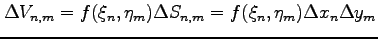 である.
ただし,
である.
ただし,
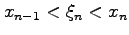 ,
,
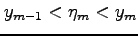 とする.
よって,
曲面
とする.
よって,
曲面 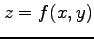 と領域
と領域 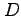 とではさまれた領域の
符合付き体積は
とではさまれた領域の
符合付き体積は
で与えられる. これを 2 変数関数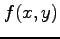 に対する
2 重積分または面積分という.
に対する
2 重積分または面積分という.
を
とする. 各小領域
の
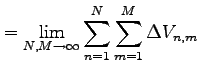 |
||
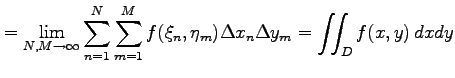 |
||
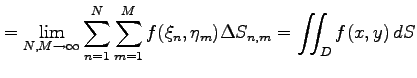 |
で与えられる. これを 2 変数関数
![\includegraphics[width=0.5\textwidth]{rect-area.eps}](img1964.png) |
![\includegraphics[width=0.5\textwidth]{volume.eps}](img1965.png)
|
注意 3.4 (領域の面積の向き)
定積分では積分区間に向きを導入し,
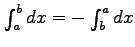 となるが,
多重積分では,
微小領域の面積
となるが,
多重積分では,
微小領域の面積
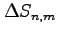 は正のみである.
例えば
は正のみである.
例えば 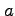 と
と 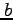 とを入れ替えて
とを入れ替えて
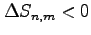 となることは
許されない.
となることは
許されない.
定義 3.5 (2 重積分)
任意の領域  に対する 2 重積分は,
領域
に対する 2 重積分は,
領域 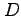 を含む長方形領域
を含む長方形領域 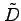 を考え,
関数
を考え,
関数
を導入し,
と定義する.
![$\displaystyle \tilde{f}(x,y)= \left\{ \begin{array}{ll} f(x,y) & (x,y)\in D \\ [1ex] 0 & (x,y)\not\in D \end{array}\right.$](img1969.png) |
を導入し,
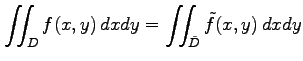 |
と定義する.
注意 3.6 (多重積分と領域の面積)
被積分関数が 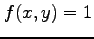 のとき,
のとき,
は領域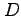 の面積となる.
の面積となる.
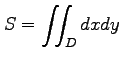 |
は領域
定義 3.7 (3 重積分)
3 変数関数 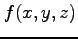 に対する3 重積分は
に対する3 重積分は
と定義される.
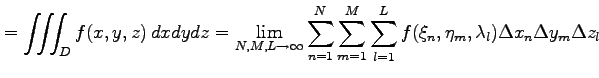 |
||
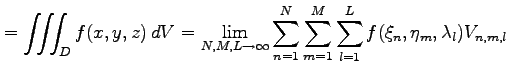 |
と定義される.
注意 3.8 (多重積分と領域の面積)
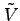 は4 次元の符合付き体積を表す,
は4 次元の符合付き体積を表す,
は領域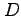 の体積を表す.
の体積を表す.
また,
被積分関数が
![]() のとき,
のとき,
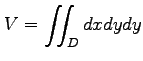 |
は領域
定義 3.9 (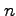 重積分)
同様にして定義される
重積分)
同様にして定義される
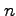 変数関数
変数関数
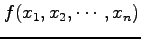 に対する
に対する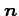 重積分は
重積分は
と表記する.
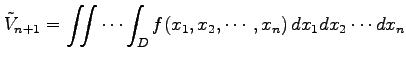 |
と表記する.
注意 3.10 (多重積分と領域の面積)
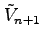 は
は 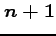 次元の符合付き体積を表す,
次元の符合付き体積を表す,
は領域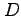 の
の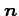 次元の体積を表す.
次元の体積を表す.
また,
![]() のとき,
のとき,
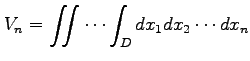 |
は領域
定義 3.11 (多重積分)
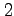 重積分,
重積分,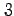 重積分,
重積分, のことを総称して,
多重積分または重積分という.
のことを総称して,
多重積分または重積分という.
平成21年1月14日