2.46 2 変数関数の極大値と極小値の判定
定理 2.217 (極値)
関数 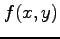 において点
において点 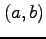 が
が
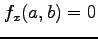 ,
,
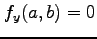 をみたすとき,
をみたすとき,
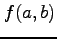 が極値となるための判定条件は次の通りである.
ただし,
が極値となるための判定条件は次の通りである.
ただし,
とおく.
と表される. ただし,簡単のために
とおいた.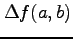 を
を 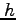 の 2 次多項式
の 2 次多項式
であるとみると,この判別式は
である.よって,
が成り立つ.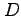 が正のとき
が正のとき 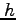 に応じて
に応じて
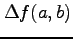 は正と負と両方の値をとりうる.
よって,
は正と負と両方の値をとりうる.
よって,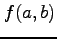 は極値とはならない.
また,
は極値とはならない.
また,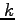 の 2 次多項式と考えたときも同様の結果を得る.
の 2 次多項式と考えたときも同様の結果を得る.
とおく.
- (i).
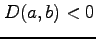 ,
,
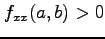 のとき,
のとき,
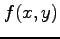 は点
は点 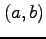 で極小値をとる.
で極小値をとる.
- (ii).
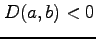 ,
,
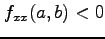 のとき,
のとき,
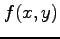 は点
は点 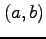 で極大値をとる.
で極大値をとる.
- (iii).
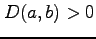 のとき,
のとき,
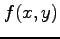 は点
は点 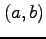 で極値をとらない.
で極値をとらない.
- (iv).
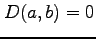 のとき,個別に判定する.
のとき,個別に判定する.
(証明)
点 ![]() から点
から点 ![]() への増分を
への増分を
![]() とする.
とする.
![]() をテイラー展開し,
をテイラー展開し,
![]() ,
,
![]() であることを
用いると,
であることを
用いると,
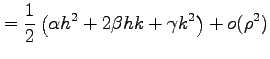 |
と表される. ただし,簡単のために
とおいた.
であるとみると,この判別式は
である.よって,
が成り立つ.
例 2.218 (極値の計算例)
関数
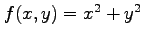 の極値を求める.
連立方程式
の極値を求める.
連立方程式
を解くと極値の候補として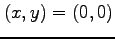 を得る.このとき,
を得る.このとき,
となる. よって,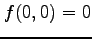 は極小値である.
は極小値である.
を解くと極値の候補として
となる. よって,
例 2.219 (極値の計算例)
関数
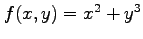 の極値を求める.
連立方程式
の極値を求める.
連立方程式
を解くと極値の候補として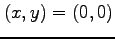 を得る.このとき,
を得る.このとき,
となる.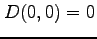 であるから判別式
であるから判別式 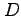 を用いて極値となるかは判定できない.
そこで,点
を用いて極値となるかは判定できない.
そこで,点 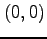 と
その近傍の点
と
その近傍の点 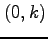 ,
, 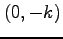 を考える.
ただし,
を考える.
ただし, 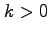 とする.
このとき,
とする.
このとき,
が成り立つ. 点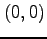 から
から 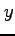 軸正の方向には増加傾向であり,
軸正の方向には増加傾向であり,
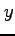 軸負の方向には減少傾向となるので,
軸負の方向には減少傾向となるので,
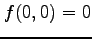 は極値ではない.
は極値ではない.
![\includegraphics[width=0.7\textwidth]{kyokuchi.eps}](img1748.png)
を解くと極値の候補として
となる.
が成り立つ. 点
![\includegraphics[width=0.7\textwidth]{kyokuchi.eps}](img1748.png)
例 2.220 (極値の計算例)
関数
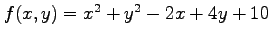 の極値を求める.
連立方程式
の極値を求める.
連立方程式
を解くと極値の候補として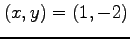 を得る.このとき,
を得る.このとき,
となる. よって,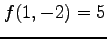 は極小値である.
は極小値である.
を解くと極値の候補として
となる. よって,
例 2.221 (極値の計算例)
関数
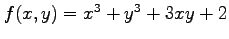 の極値を求める.
連立方程式
の極値を求める.
連立方程式
を解く. 第 1 式を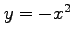 と変形して第 2 式に代入すると
と変形して第 2 式に代入すると
となる.これを解くと,極値の候補として
を得る.このとき,
を用いて極値であるか判定する. まず,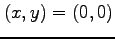 の場合.
の場合.
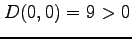 より
より 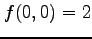 は極値ではない.
次に,
は極値ではない.
次に,
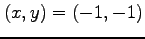 の場合.
の場合.
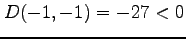 ,
,
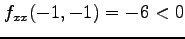 より,
より,
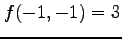 は極大値である.
は極大値である.
![\includegraphics[width=0.7\textwidth]{kyokuchi2.eps}](img1754.png)
を解く. 第 1 式を
となる.これを解くと,極値の候補として
を得る.このとき,
を用いて極値であるか判定する. まず,
![\includegraphics[width=0.7\textwidth]{kyokuchi2.eps}](img1754.png)
平成21年1月14日