2.9 演習問題 〜 偏微分
問 2.41 (偏導関数)
関数 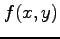 の偏導関数
の偏導関数 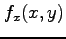 ,
, 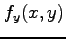 の定義を述べよ.
の定義を述べよ.
問 2.42 (偏微係数)
関数 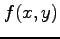 の偏導関数と点
の偏導関数と点 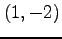 における偏微係数を求めよ.
における偏微係数を求めよ.
(1)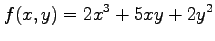 (2)
(2)
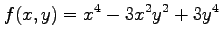
(3)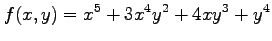 (4)
(4)
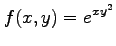 (5)
(5)
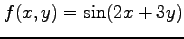
(1)
(3)
問 2.43 (1 階偏導関数)
次の関数の  階偏導関数を全て求めよ.
階偏導関数を全て求めよ.
(1)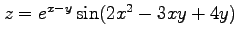 (2)
(2)
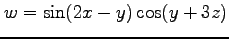 (3)
(3)
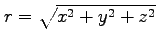
(4)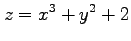 (5)
(5)
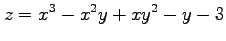 (6)
(6)
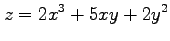
(7)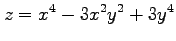 (8)
(8)
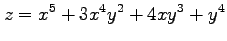 (9)
(9)
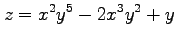
(10)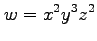 (11)
(11)
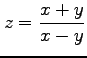 (12)
(12)
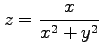 (13)
(13)
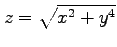
(14)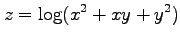 (15)
(15)
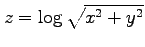 (16)
(16)
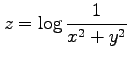 (17)
(17)
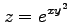
(18)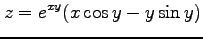 (19)
(19)
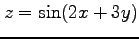 (20)
(20)
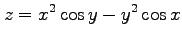
(21)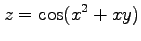 (22)
(22)
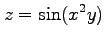 (23)
(23)
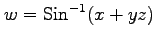 (24)
(24)
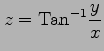
(25)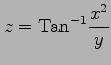 (26)
(26)
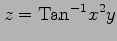
(1)
(4)
(7)
(10)
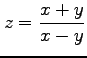 (12)
(12)
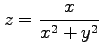 (13)
(13)
(14)
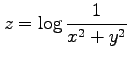 (17)
(17)
(18)
(21)
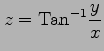
(25)
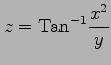 (26)
(26)
問 2.44 (偏導関数)
次の関係式が成り立つことを示せ.
(1)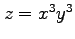 ,
,
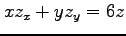 (2)
(2)
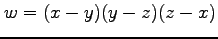 ,
,
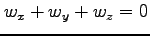
(1)
問 2.45 (偏導関数)
関数 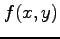 の高階偏導関数を計算し,
の高階偏導関数を計算し,
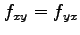 ,
,
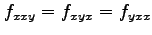 ,
,
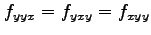 となることを確認せよ.
となることを確認せよ.
(1)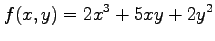 (2)
(2)
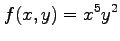 (3)
(3)
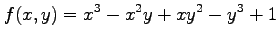
(4)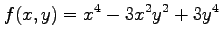 (5)
(5)
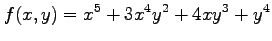 (6)
(6)
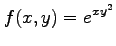
(7)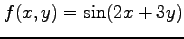 (8)
(8)
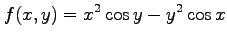 (9)
(9)
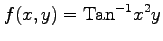
(1)
(4)
(7)
問 2.46 (2 階偏導関数)
次の関数の 1 階, 2 階偏導関数を全て求めよ.
(1)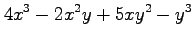 (2)
(2)
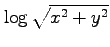 (3)
(3)
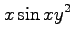 (4)
(4)
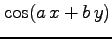
(5)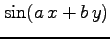 (6)
(6)
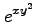
(7)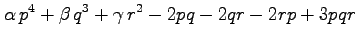 (
(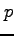 ,
, 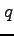 ,
, 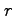 について)
について)
(1)
(5)
(7)
問 2.47 (3 階偏導関数)
次の関数の 1 階, 2 階, 3 階偏導関数を全て求めよ.
(1)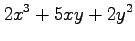 (2)
(2)
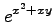
(1)
問 2.48 (偏微分)
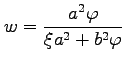 であるとき
であるとき
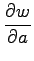 ,
,
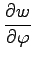 ,
,
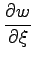 ,
,
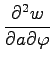 ,
,
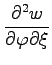 を求めよ.
を求めよ.
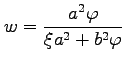 であるとき
であるとき
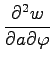 ,
,
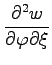 を求めよ.
を求めよ.
平成21年1月14日