2.6 偏微分
定義 2.25 (偏微分,偏微分係数)
関数 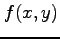 の点
の点 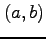 において,
極限
において,
極限
が存在するとき, 関数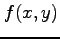 は
点
は
点 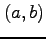 において,
において,
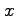 または
または 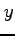 に関して
偏微分可能(partial differentiable)
であるという.
この極限を
偏微分係数(partial differential coefficient)という.
に関して
偏微分可能(partial differentiable)
であるという.
この極限を
偏微分係数(partial differential coefficient)という.
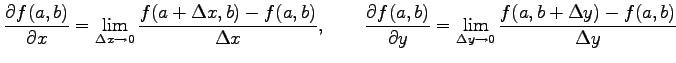 |
が存在するとき, 関数
定義 2.26 (偏動関数)
定義 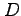 内の任意の点
内の任意の点 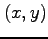 に対して極限
に対して極限
が存在するとき, これらを偏導関数(partial derivative)という. 偏導関数を求める操作を偏微分するという.
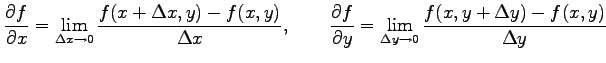 |
が存在するとき, これらを偏導関数(partial derivative)という. 偏導関数を求める操作を偏微分するという.
注意 2.27 (偏微分の記号)
関数 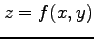 の偏導関数は
の偏導関数は
と表記する.
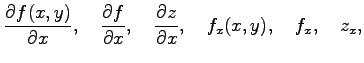 |
||
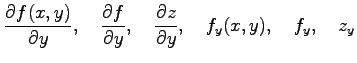 |
と表記する.
注意 2.28 (偏微分)
関数 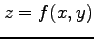 のグラフは
のグラフは 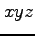 空間内の曲面となる.
このグラフと平面
空間内の曲面となる.
このグラフと平面 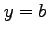 との共有点のグラフは
との共有点のグラフは
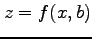 で与えられる曲線となる.
このとき関数
で与えられる曲線となる.
このとき関数 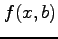 は
は 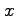 についての 1 変数関数であるから,
についての 1 変数関数であるから,
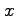 について微分すれば曲線
について微分すれば曲線 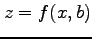 の
傾き
の
傾き 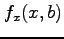 が得られる.
が得られる.
同様にしてグラフ ![]() と平面
と平面 ![]() との共有点の曲線
との共有点の曲線 ![]() は,
は,
![]() についての 1 変数関数であるから,
についての 1 変数関数であるから,
![]() について微分すれば曲線
について微分すれば曲線 ![]() の傾き
の傾き ![]() が得られる.
が得られる.
注意 2.29 (偏微分)
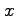 に関する偏微分の定義式において,
に関する偏微分の定義式において,
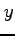 は定数と考えて
は定数と考えて 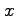 方向の極限のみを考えている.
同様にして,
方向の極限のみを考えている.
同様にして,
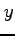 に関する偏微分の定義式は,
に関する偏微分の定義式は,
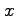 は定数と考えて
は定数と考えて 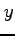 方向の極限のみを考えている.
このとき定義式は
方向の極限のみを考えている.
このとき定義式は 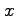 と
と 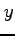 についての
1 変数関数の微分とそれぞれ等価となる.
よって,ひとつの独立変数を除いて他のすべての独立変数を
定数と考えて 1 変数関数の微分をすればよい.
についての
1 変数関数の微分とそれぞれ等価となる.
よって,ひとつの独立変数を除いて他のすべての独立変数を
定数と考えて 1 変数関数の微分をすればよい.
例 2.30 (偏微分)
関数
を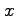 で偏微分すると,
で偏微分すると,
となり,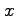 に関する偏導関数が得られる.
に関する偏導関数が得られる.
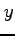 で偏微分すると,
で偏微分すると,
となり,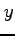 に関する偏導関数が得られる.
に関する偏導関数が得られる.
を
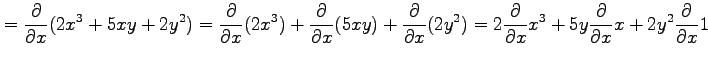 |
||
となり,
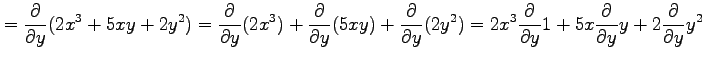 |
||
となり,
例 2.31 (偏微分係数)
関数
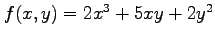 の点
の点 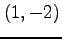 における偏微分係数は
における偏微分係数は
となる.
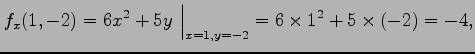 |
||
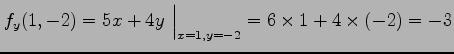 |
となる.
例 2.32 (偏微分)
関数
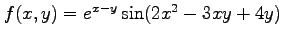 の
偏導関数は,
の
偏導関数は,
となる.
となる.
平成21年1月14日