4.16 等比級数
例 4.50 (等比級数)
等比数列
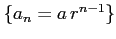 の無限和を
等比級数(geometrical progression series)と呼び,
の無限和を
等比級数(geometrical progression series)と呼び,
と書き表す. 等比級数は
となる.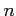 部分和
部分和
を考える.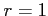 のとき,
のとき,
となる. つぎに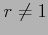 のとき,等式
のとき,等式
を用いると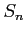 は
は
と書ける. 以上より
となる. ただし無限大の符号は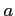 の符号
の符号
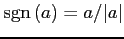 で決まる.
証明終り.
で決まる.
証明終り.
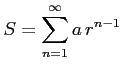 |
と書き表す. 等比級数は
![$\displaystyle S=\left\{ \begin{array}{ll} \displaystyle{\frac{a}{1-r}} & (\vert r\vert< 1) \\ [1em] \text{発散} & (\vert r\vert\ge 1) \end{array} \right.$](img1706.png) |
となる.
(証明) 第
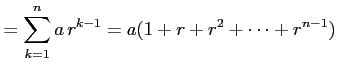 |
を考える.
となる. つぎに
を用いると
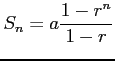 |
と書ける. 以上より
![$\displaystyle S=\lim_{n\to\infty}S_{n}= \left\{ \begin{array}{lc} \displaystyle...
...& (-1<r<1)\\ [2ex] \displaystyle{\text{不確定}} & (r\leq-1) \end{array} \right.$](img1713.png) |
となる. ただし無限大の符号は
問 4.51 (1を根にもつ多項式の因数分解)
次の等式を示せ.
注意 4.52 (初項が異なる級数)
級数が
と定義されるときの値を考える. 部分和は
となるから, 結局級数は
と得られる.
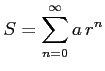 |
と定義されるときの値を考える. 部分和は
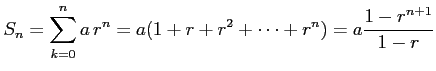 |
となるから, 結局級数は
![$\displaystyle S= \lim_{n\to\infty}S_{n}= \lim_{n\to\infty}a\frac{1-r^{n+1}}{1-r...
...(\vert r\vert<1) \\ [1ex] \text{発散} & (\vert r\vert\geq1) \end{array} \right.$](img1718.png) |
と得られる.
注意 4.53 (等比級数の有理式表現)
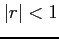 のとき
のとき
となる. この式は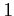 を
を 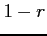 で割ることでも導出される.
すなわち,
で割ることでも導出される.
すなわち,
のように低次項を主項として割り算を無限回続ける.
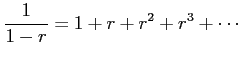 |
となる. この式は
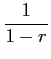 |
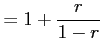 |
|
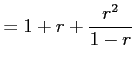 |
||
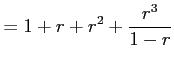 |
||
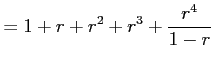 |
||
のように低次項を主項として割り算を無限回続ける.
例 4.54 (等比級数の具体例)
等比級数
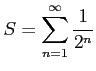 を考える.
部分和は
を考える.
部分和は
となるので,級数は
と得られる. または,等比級数の公比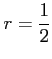 が
が 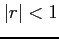 をみたすので,
級数は収束する.よって,公式を用いて級数は
をみたすので,
級数は収束する.よって,公式を用いて級数は
と得られる.
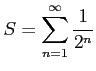 を考える.
部分和は
を考える.
部分和は
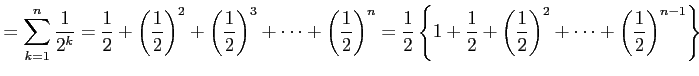 |
||
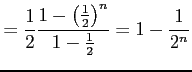 |
となるので,級数は
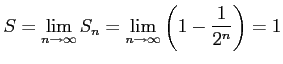 |
と得られる. または,等比級数の公比
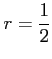 が
が 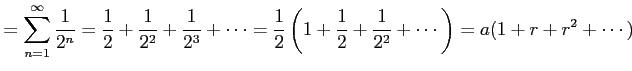 |
||
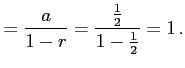 |
と得られる.
例 4.55 (等比級数の具体例)
級数
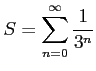 を考える.
部分和は
を考える.
部分和は
であるから,級数は
と得られる. または, 比級数の公比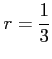 が
が 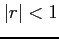 をみたすので,
級数は収束する.よって,公式を用いて級数は
をみたすので,
級数は収束する.よって,公式を用いて級数は
と得られる.
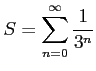 を考える.
部分和は
を考える.
部分和は
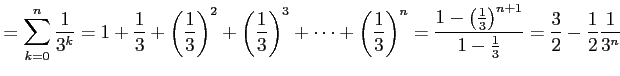 |
であるから,級数は
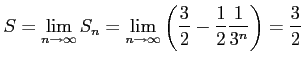 |
と得られる. または, 比級数の公比
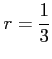 が
が 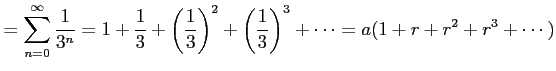 |
||
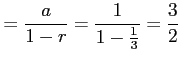 |
と得られる.
例 4.56 (等比級数の具体例)
(証明)
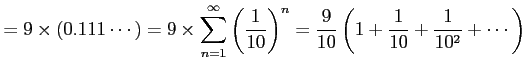 |
||
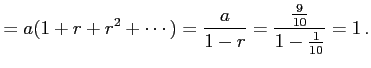 |
平成21年6月1日