2.35 sinc 関数を用いた極限の計算
公式 2.134 (sinc関数)
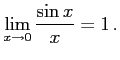 |
例 2.135 (関数の極限の計算例)
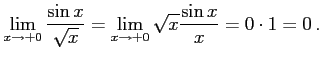 |
例 2.136 (関数の極限の計算例)
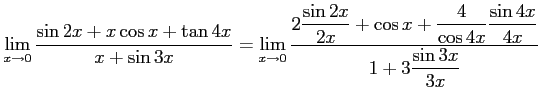 |
||
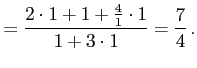 |
例 2.137 (関数の極限の計算例)
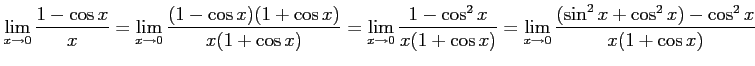 |
||
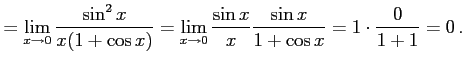 |
平成21年6月1日
2.35 sinc 関数を用いた極限の計算
公式 2.134 (sinc関数)
例 2.135 (関数の極限の計算例)
例 2.136 (関数の極限の計算例)
例 2.137 (関数の極限の計算例)
平成21年6月1日