6.32 演習 〜 広義積分
問 6.171 (広義積分)
次の広義積分の値を求めよ.
(1)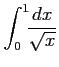 (2)
(2)
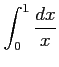 (3)
(3)
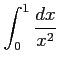 (4)
(4)
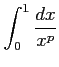 (
(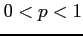 )
(5)
)
(5)
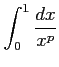 (
(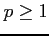 )
)
(6)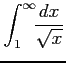 (7)
(7)
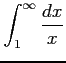 (8)
(8)
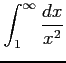 (9)
(9)
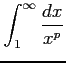 (
(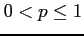 )
(10)
)
(10)
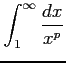 (
(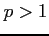 )
)
(11)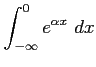 (
(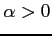 )
(12)
)
(12)
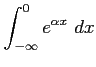 (
(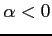 )
(13)
)
(13)
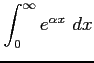 (
(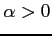 )
)
(14)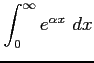 (
(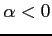 )
(15)
)
(15)
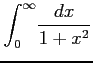 (16)
(16)
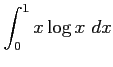 (17)
(17)
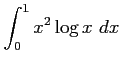
(18)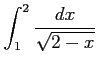 (19)
(19)
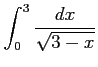 (20)
(20)
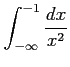 (21)
(21)
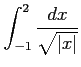 (22)
(22)
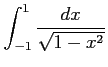
(23)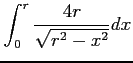 (
(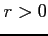 )
(24)
)
(24)
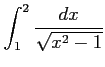 (25)
(25)
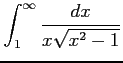 (26)
(26)
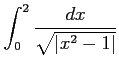
(27)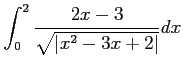 (28)
(28)
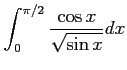 (29)
(29)
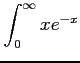 (30)
(30)
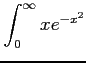
(31)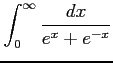
(1)
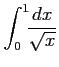 (2)
(2)
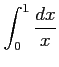 (3)
(3)
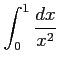 (4)
(4)
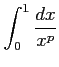 (
(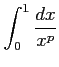 (
((6)
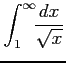 (7)
(7)
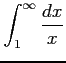 (8)
(8)
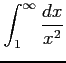 (9)
(9)
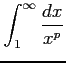 (
(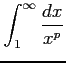 (
((11)
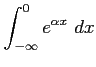 (
(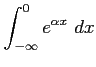 (
(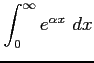 (
((14)
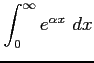 (
(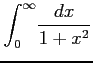 (16)
(16)
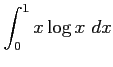 (17)
(17)
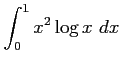
(18)
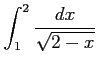 (19)
(19)
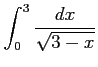 (20)
(20)
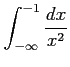 (21)
(21)
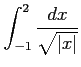 (22)
(22)
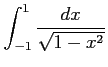
(23)
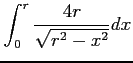 (
(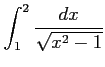 (25)
(25)
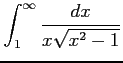 (26)
(26)
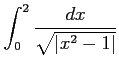
(27)
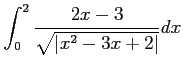 (28)
(28)
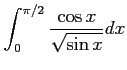 (29)
(29)
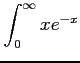 (30)
(30)
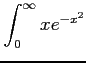
(31)
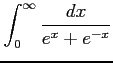
問 6.172 (広義積分)
定積分
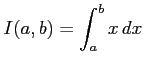 を計算し,
条件
を計算し,
条件 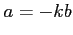 (
(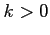 ) を課した後に
極限
) を課した後に
極限
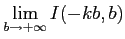 を求める.
を求める.
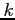 が次の範囲内にあるとき極限をそれぞれ求めよ.
が次の範囲内にあるとき極限をそれぞれ求めよ.
(1) (2)
(2) 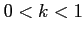 (3)
(3) 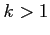
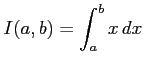 を計算し,
条件
を計算し,
条件 (1)
問 6.173 (コーシーの主値積分)
次の広義積分とコーシー主値積分の違いに注意して積分の値を求めよ.
(1)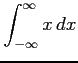 (2)
(2)
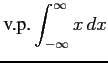 (3)
(3)
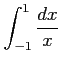 (4)
(4)
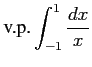 (5)
(5)
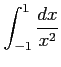
(6)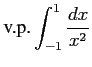 (7)
(7)
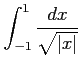 (8)
(8)
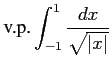 (9)
(9)
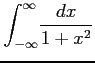 (10)
(10)
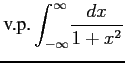
(1)
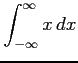 (2)
(2)
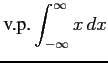 (3)
(3)
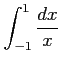 (4)
(4)
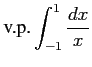 (5)
(5)
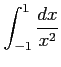
(6)
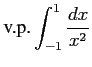 (7)
(7)
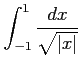 (8)
(8)
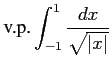 (9)
(9)
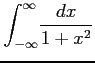 (10)
(10)
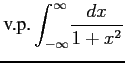
問 6.174 (広義積分)
広義積分を用いて次の級数が収束するか発散するか議論せよ.
(1)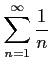 (2)
(2)
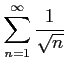 (3)
(3)
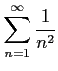 (4)
(4)
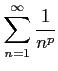 (
(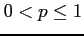 )
(5)
)
(5)
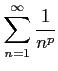 (
(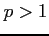 )
)
(1)
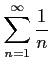 (2)
(2)
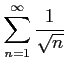 (3)
(3)
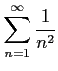 (4)
(4)
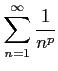 (
(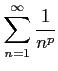 (
(
問 6.175 (広義積分)
次の広義積分は収束するか発散するか議論せよ.
(1)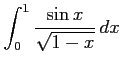 (2)
(2)
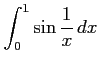 (3)
(3)
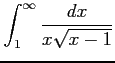 (4)
(4)
![$ \displaystyle{\int_{2}^{\infty}\frac{dx}{\sqrt[3]{x(x-1)}}}$](img3720.png) (5)
(5)
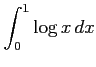
(6)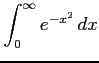 (7)
(7)
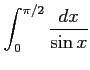 (8)
(8)
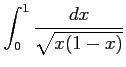 (9)
(9)
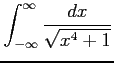 (10)
(10)
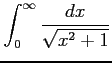
(1)
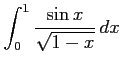 (2)
(2)
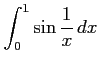 (3)
(3)
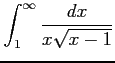 (4)
(4)
![$ \displaystyle{\int_{2}^{\infty}\frac{dx}{\sqrt[3]{x(x-1)}}}$](img3720.png) (5)
(5)
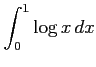
(6)
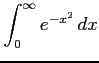 (7)
(7)
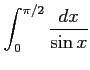 (8)
(8)
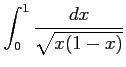 (9)
(9)
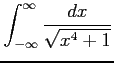 (10)
(10)
平成21年6月1日