6.4 置換積分法
定理 6.6 (置換積分法)
積分変数を 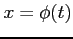 と変換すると
と変換すると
となる. また逆に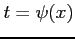 とおくと,
とおくと,
となる. この積分の方法を 置換積分法(integration by substitution)という.
となる.両辺を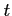 で積分すると
で積分すると
を得る.左辺は
であるから証明終了.
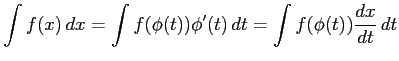 |
となる. また逆に
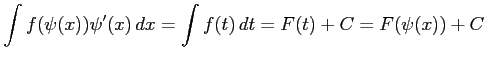 |
となる. この積分の方法を 置換積分法(integration by substitution)という.
(証明)関数 ![]() を
を ![]() の原始関数とする.
変数
の原始関数とする.
変数 ![]() を
を ![]() と変数変換する.
このとき
と変数変換する.
このとき
![]() は
合成関数の微分則より
は
合成関数の微分則より
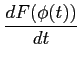 |
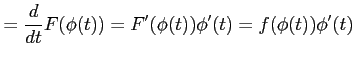 |
となる.両辺を
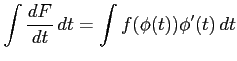 |
を得る.左辺は
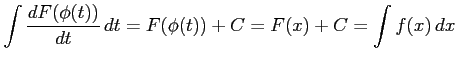 |
であるから証明終了.
例 6.7 (置換積分の使用例)
不定積分
を計算する.まず
と変数変換する.このとき両辺を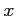 で微分すると
で微分すると
であるので
を得る.これより置換積分法を用いると不定積分は
となる.変数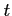 を
を 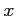 に戻すと
に戻すと
を得る.
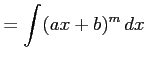 |
を計算する.まず
と変数変換する.このとき両辺を
であるので
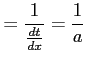 |
を得る.これより置換積分法を用いると不定積分は
![$\displaystyle = \int t^{m}\frac{dx}{dt}\,dt= \int t^{m}\frac{1}{a}\,dt= \frac{1...
...[3ex] \displaystyle{\frac{1}{a}\log\vert t\vert+C} & (m=-1) \end{array} \right.$](img2610.png) |
となる.変数
![$\displaystyle = \left\{ \begin{array}{ll} \displaystyle{\frac{(ax+b)^{m+1}}{a(m...
...x] \displaystyle{\frac{1}{a}\log\vert ax+b\vert+C} & (m=-1) \end{array} \right.$](img2611.png) |
を得る.
置換積分は慣れてくれば変数変換を省略して計算をする. 次のように式変形を行なう:
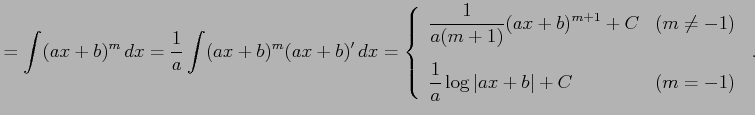 |
例 6.8 (置換積分の使用例)
ここで,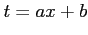 とおき,
とおき,
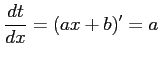 ,
,
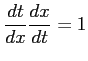 を用いた.
を用いた.
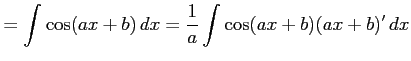 |
||
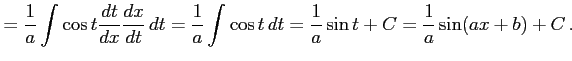 |
ここで,
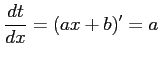 ,
,
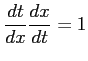 を用いた.
を用いた.
例 6.9 (置換積分の使用例)
ここで,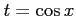 とおき,
とおき,
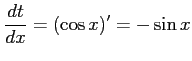 ,
,
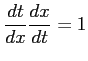 を用いた.
を用いた.
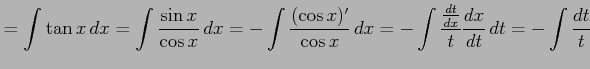 |
||
ここで,
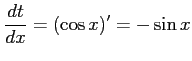 ,
,
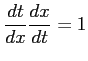 を用いた.
を用いた.
例 6.10 (置換積分の使用例)
ここで,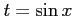 とおき,
とおき,
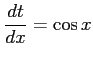 ,
,
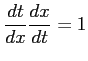 を用いた.
を用いた.
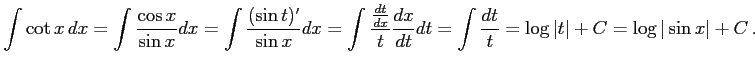 |
ここで,
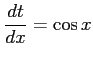 ,
,
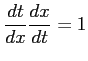 を用いた.
を用いた.
例 6.11 (置換積分の使用例)
ここで,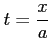 とおき,
とおき,
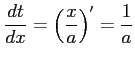 ,
,
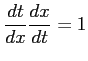 を用いた.
を用いた.
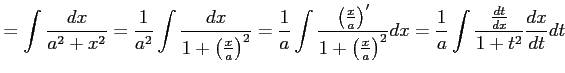 |
||
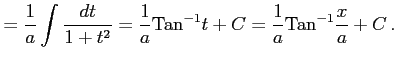 |
ここで,
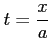 とおき,
とおき,
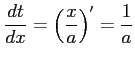 ,
,
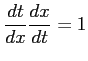 を用いた.
を用いた.
例 6.12 (置換積分の使用例)
ここで,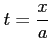 とおき,
とおき,
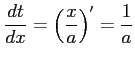 ,
,
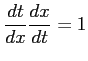 を用いた.
を用いた.
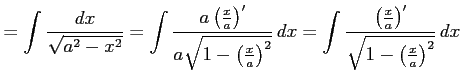 |
||
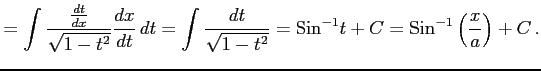 |
ここで,
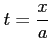 とおき,
とおき,
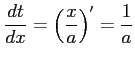 ,
,
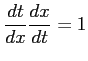 を用いた.
を用いた.
例 6.13 (置換積分の使用例)
ここで,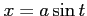 とおき,
とおき,
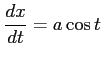 を用いて積分し,
を用いて積分し,
を用いて変形した.
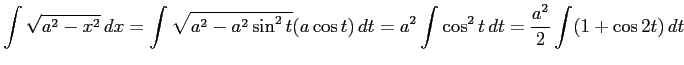 |
||
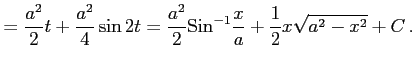 |
ここで,
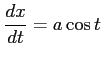 を用いて積分し,
を用いて積分し,
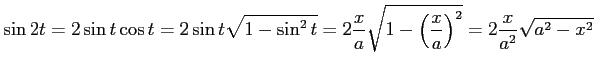 |
を用いて変形した.
例 6.14 (置換積分の使用例)
これで不定積分は得られたが他の表現も考える. 逆双曲線関数は
とも表される.これを用いると不定積分は
となる.またこれを変形すると
となる.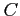 は任意の定数なので
は任意の定数なので 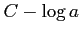 をあらためて
をあらためて 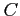 と
おき直すと
と
おき直すと
を得る. 以上得られた結果は 任意定数分の不定性を除けば全て同じ不定積分である.
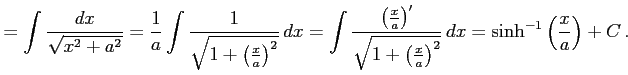 |
これで不定積分は得られたが他の表現も考える. 逆双曲線関数は
とも表される.これを用いると不定積分は
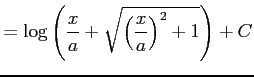 |
となる.またこれを変形すると
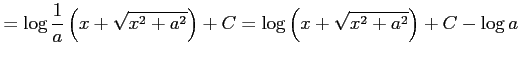 |
となる.
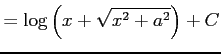 |
を得る. 以上得られた結果は 任意定数分の不定性を除けば全て同じ不定積分である.
注意 6.15 (不定積分の関数の表現)
不定積分は計算の方法により得られる結果が一見すると
違うときがある.
これは不定積分が任意定数の不定性をもつためである.
注意が必用である.
例 6.16 (置換積分の使用例)
ここで,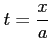 とおき,
とおき,
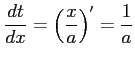 ,
,
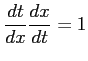 を用いた.
を用いた.
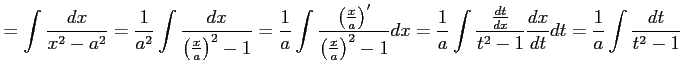 |
||
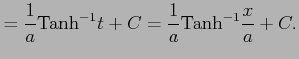 |
ここで,
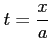 とおき,
とおき,
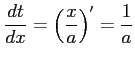 ,
,
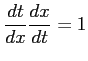 を用いた.
を用いた.
例 6.17 (置換積分の使用例)
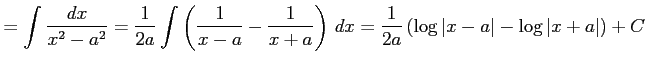 |
||
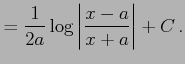 |
例 6.18 (置換積分の使用例)
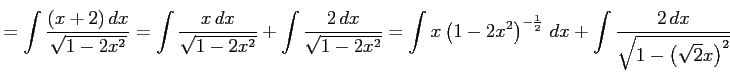 |
||
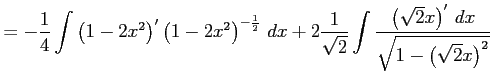 |
||
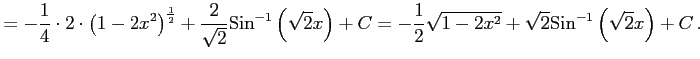 |
例 6.19 (置換積分の計算例)
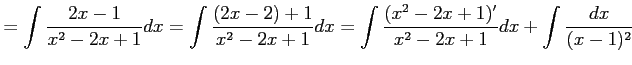 |
||
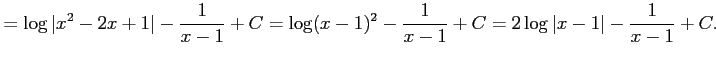 |
例 6.20 (置換積分の計算例)
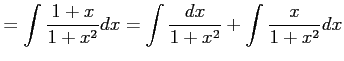 |
||
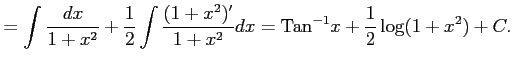 |
例 6.21 (置換積分の計算例)
ここで,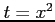 とおき,
とおき,
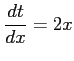 ,
,
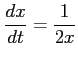 を用いた.
を用いた.
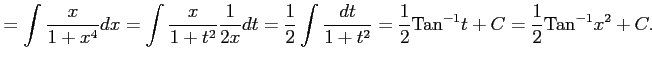 |
ここで,
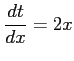 ,
,
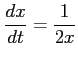 を用いた.
を用いた.
例 6.22 (置換積分の計算例)
ここで,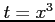 とおき,
とおき,
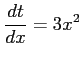 ,
,
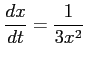 を用いた.
を用いた.
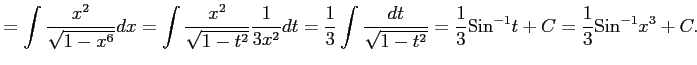 |
ここで,
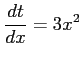 ,
,
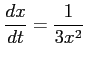 を用いた.
を用いた.
例 6.23 (置換積分の計算例)
ここで,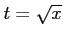 ,
,  とおき,
とおき,
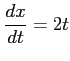 を用いた.
を用いた.
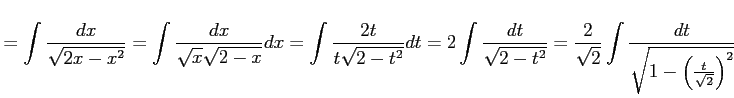 |
||
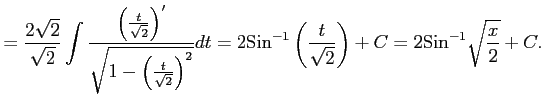 |
ここで,
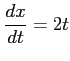 を用いた.
を用いた.
平成21年6月1日