5.14 オイラーの関係式
注意 5.32 (三角関数と指数関数)
三角関数と指数関数は
の関係にある. これをオイラーの関係式という. ここで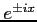 は複素指数関数である.
複素指数関数は複素数
は複素指数関数である.
複素指数関数は複素数 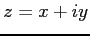 に対して
に対して
と定義される. 右辺は複素べき級数である. この定義より関係式が自然に導出される. このとき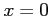 とし
とし 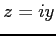 とおく.
すると
とおく.
すると
を得る. 同様に とおくと
とおくと
を得る.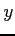 を
を 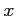 に置き換えることで,最初の関係式を得る.
に置き換えることで,最初の関係式を得る.
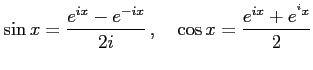 |
の関係にある. これをオイラーの関係式という. ここで
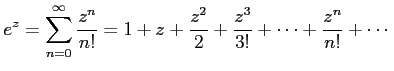 |
と定義される. 右辺は複素べき級数である. この定義より関係式が自然に導出される. このとき
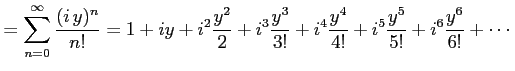 |
||
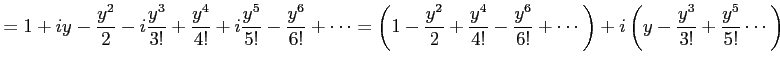 |
||
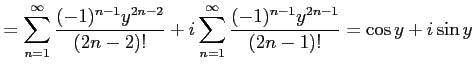 |
を得る. 同様に
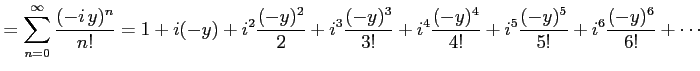 |
||
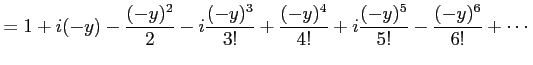 |
||
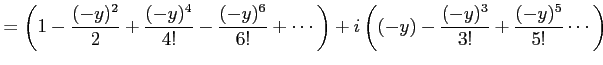 |
||
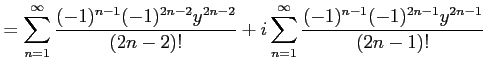 |
||
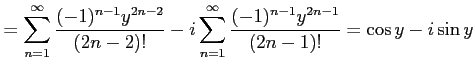 |
を得る.
平成21年6月1日