5.11 割り算によるテイラー級数の計算
例 5.21 (テイラー級数の計算例)
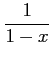 |
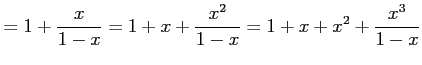 |
|
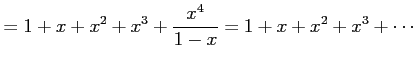 |
例 5.22 (テイラー級数の計算例)
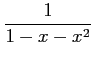 |
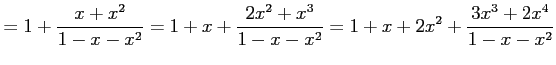 |
|
例 5.23 (テイラー級数の計算例)
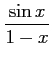 |
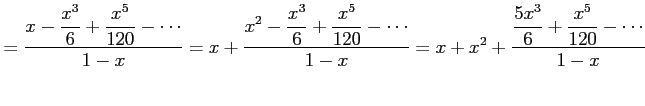 |
|
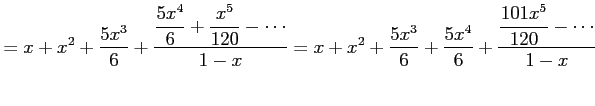 |
||
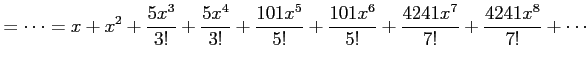 |
例 5.24 (テイラー級数の計算例)
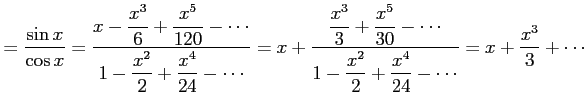 |
例 5.25 (テイラー級数の計算例)
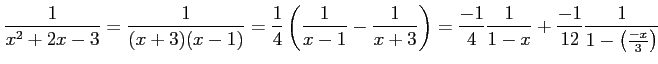 |
||
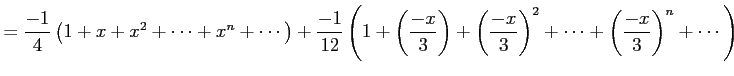 |
||
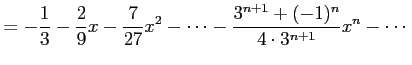 |
平成21年6月1日