5.3 指数関数のテイラー級数
例 5.3 (指数関数のテイラー級数)
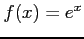 とおく.
導関数を計算すると
とおく.
導関数を計算すると
となる. 点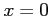 における微分係数は
における微分係数は
である. よってテーラー級数は
と求まる. べき級数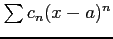 の
収束半径
の
収束半径 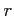 を求める.
係数は
を求める.
係数は
であるから, 収束半径として
を得る.
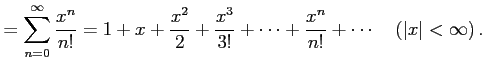 |
(導出)
となる. 点
である. よってテーラー級数は
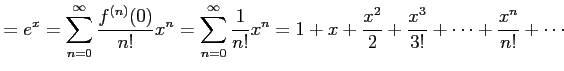 |
と求まる. べき級数
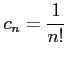 |
であるから, 収束半径として
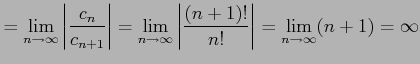 |
を得る.
例 5.4 (指数関数のテイラー級数)
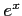 の
の 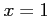 まわりでのテイラー級数は,
まわりでのテイラー級数は,
より,
である. 収束半径は
である.
より,
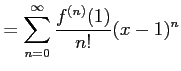 |
||
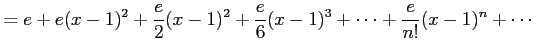 |
である. 収束半径は
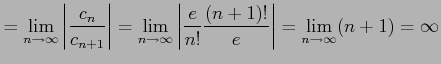 |
である.
平成21年6月1日