4.24 直線の線形変換
問 4.113 (直線の線形変換)
直線 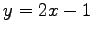 を線形変換
を線形変換
で写してできる直線を求めよ. また,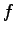 で動かない点を求めよ.
で動かない点を求めよ.
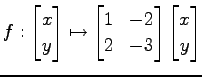 |
で写してできる直線を求めよ. また,
問 4.114 (直線の線形変換)
線形変換
は直線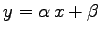 をある 1 点に写すとする.
このとき
をある 1 点に写すとする.
このとき 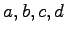 の条件を求めよ.
また,その点を求めよ.
の条件を求めよ.
また,その点を求めよ.
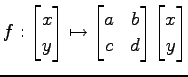 |
は直線
注意 4.115 (直線の線形変換)
線形変換
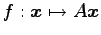 により,
直線を直線へ写すときは
により,
直線を直線へ写すときは
である. 直線を 1 点へ写すときは
である.
である. 直線を 1 点へ写すときは
である.
平成20年2月2日