4.17 直交変換と直交行列
定理 4.81 (直交変換と直交行列)
線形変換 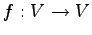 が
直交変換であることと,
が
直交変換であることと,
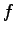 の表現行列が直交行列であることとは,
必要十分条件である.
の表現行列が直交行列であることとは,
必要十分条件である.
をみたす. この式より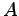 は
は 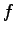 の表現行列ともみなせる.
よって直交変換
の表現行列ともみなせる.
よって直交変換 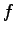 の表現行列
の表現行列 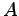 は直交行列である.
(十分条件)
は直交行列である.
(十分条件)
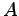 を直交行列とする.
を直交行列とする.
とおく.このとき
をみたす.よって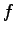 は直交変換である.
は直交変換である.
(証明)
(必要条件)
![]() ,
, ![]() ,
,
![]() を
を
![]() の正規直交基底とする.
の正規直交基底とする.
![]() が直交変換であるとき,
が直交変換であるとき,
![]() ,
, ![]() ,
,
![]() も
正規直交基底となる.
また,
正規直交基底
も
正規直交基底となる.
また,
正規直交基底
![]() ,
, ![]() ,
,
![]() から
正規直交基底
から
正規直交基底
![]() ,
, ![]() ,
,
![]() への
基底の変換行列
への
基底の変換行列 ![]() は直交行列であり,
は直交行列であり,
をみたす. この式より
とおく.このとき
をみたす.よって
平成20年2月2日