3.1 連立 1 次方程式の行列表現

連立 1 次方程式

$$\left\{\begin{array}{rcrll} 2x & \!+\! & 3y & = & 7 \\ [.5ex] x & \!-\! & 4y & = & 9 \end{array}\right.$$ (377)

を考える． 行列を用いて書き直すと等価な方程式として

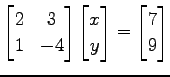$$\begin{bmatrix}2 & 3 \\ 1 & -4 \end{bmatrix} \begin{bmatrix}x \\ y \end{bmatrix}= \begin{bmatrix}7 \\ 9 \end{bmatrix}$$ (378)

を得る． 一般に変数 $n$ 個，方程式 $m$ 本の連立 1 次方程式は

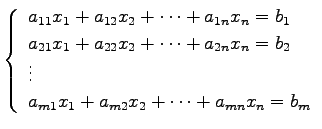$$\left\{\begin{array}{l} a_{11}x_{1}+a_{12}x_{2}+\cdots+a_{1n}x_{n... ...\ \vdots \\ a_{m1}x_{1}+a_{m2}x_{2}+\cdots+a_{mn}x_{n}=b_{m} \end{array}\right.$$ (379)

と表される． これを連立 $n$ 元 1 次方程式（simultaneous linear equations）という． 行列で書き直すと，

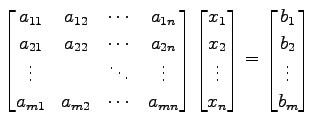$$\begin{bmatrix}a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{2... ...} \end{bmatrix}= \begin{bmatrix}b_{1} \\ b_{2} \\ \vdots \\ b_{m} \end{bmatrix}$$ (380)

となる． 行列をそれぞれ文字で置き換えて

$$A\,\vec{x}=\vec{b}\,,\qquad A=[a_{ij}]_{m\times n}\,,\qquad \vec{x}=[x_{j}]_{n\times1}\,,\qquad \vec{b}=[b_{i}]_{m\times1}\,$$ (381)

と表される． 行列により表現された方程式と 元の連立 1 次方程式は等価な方程式である．

$\vec{b}=\vec{0}$ のとき同次連立 1 次方程式または単に 同次形（homogeneous equations???）という． $\vec{b}\neq\vec{0}$ のとき非同次連立 1 次方程式または 非同次形（inhomogeneous equations???）という．

定義 3.1 (係数行列)   連立 1 次方程式 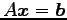$A\vec{x}=\vec{b}$ の 係数をまとめた行列

$$A = \begin{bmatrix}a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_... ...\ \vdots & & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{bmatrix}$$ (382)

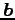を係数行列（coefficient matrix）と呼ぶ． 行列 $A$ と $\vec{b}$ を部分行列としてまとめた行列

$$[A\vert\vec{b}] = \left[\begin{array}{cccc\vert c} a_{11} & a_{12} & \cdots & a_{... ...\vdots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} & b_{m} \end{array}\right]$$ (383)

のことを拡大係数行列（enlarged coefficient matrix）と呼ぶ．

例 3.2 (連立 1 次方程式の行列表現の具体例)   連立 1 次方程式

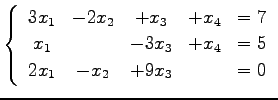$$\left\{\begin{array}{ccccc} 3x_{1} & -2x_{2} & +x_{3} & +x_{4} & ... ... & -3x_{3} & +x_{4} & =5 \\ 2x_{1} & -x_{2} & +9x_{3} & & =0 \end{array}\right.$$ (384)

の係数行列と拡大係数行列は

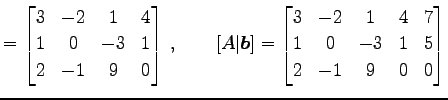$$A = \begin{bmatrix}3 & -2 & 1 & 4 \\ 1 & 0 & -3 & 1 \\ 2 & -1 & 9 &... ...ix}3 & -2 & 1 & 4 & 7 \\ 1 & 0 & -3 & 1 & 5 \\ 2 & -1 & 9 & 0 & 0 \end{bmatrix}$$ (385)

である．行列を用いて方程式を書き直すと

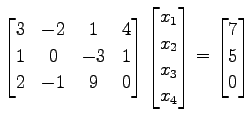$$\begin{bmatrix}3 & -2 & 1 & 4 \\ 1 & 0 & -3 & 1 \\ 2 & -1 & 9 & 0... ...x_{2} \\ x_{3} \\ x_{4} \end{bmatrix}= \begin{bmatrix}7 \\ 5 \\ 0 \end{bmatrix}$$ (386)

と表される．

問 3.3   教科書（p.18）問題1.4 1.-2.

平成20年2月2日