2.10 クロネッカーのデルタ

定義 2.40 (クロネッカーのデルタ)   記号 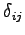$\delta_{ij}$ を

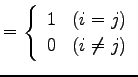$$\delta_{ij} = \left\{ \begin{array}{ll} 1 & (i=j) \\ 0 & (i\neq j) \end{array} \right.$$ (278)

と定義する． これをクロネッカーのデルタ（Kronecker's delta）と呼ぶ．

例 2.41 (クロネッカーのデルタの具体例)  

$$\delta_{11}=\delta_{22}=\delta_{33}=1$$ (279)

$$\delta_{12}=\delta_{13}=\delta_{21}=\delta_{23}= \delta_{31}=\delta_{32}=0$$ (280)

例 2.42 (クロネッカーのデルタの使用例)   単位行列は $E_{n}=[\delta_{ij}]_{n\times n}$ と表わされる． 例えば

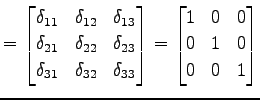$$E_{3} = \begin{bmatrix}\delta_{11} & \delta_{12} & \delta_{13} \\ \delt... ...end{bmatrix} = \begin{bmatrix}1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}$$ (281)

となる．

例 2.43 (クロネッカーのデルタの使用例)   行列 $A$ が $A=[\delta_{i+1,j}]$ と与えられるとき，

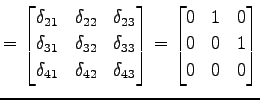$$A = \begin{bmatrix}\delta_{21} & \delta_{22} & \delta_{23} \\ \delt... ...\end{bmatrix}= \begin{bmatrix}0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \end{bmatrix}$$ (282)

となる．

平成20年2月2日