4.18 演習 〜 数列,級数
問 4.74 (数列)
次の数列について
(i)概形を書け.(ii)一般項を表せ.(iii)極限を求めよ.
(1)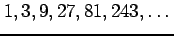 (2)
(2)
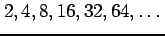 (3)
(3)
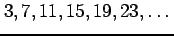 (4)
(4)
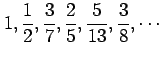
(5)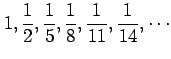 (6)
(6)
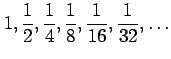 (7)
(7)
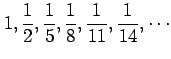 (8)
(8)
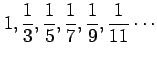
(9)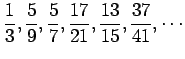 (10)
(10)
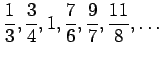 (11)
(11)
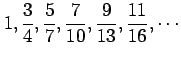
(12)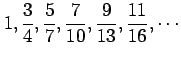 (13)
(13)
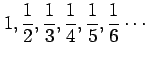
(1)
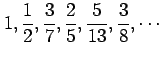
(5)
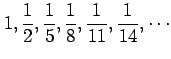 (6)
(6)
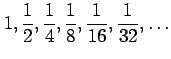 (7)
(7)
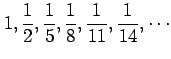 (8)
(8)
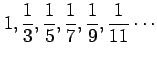
(9)
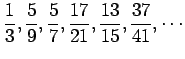 (10)
(10)
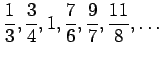 (11)
(11)
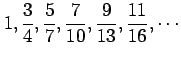
(12)
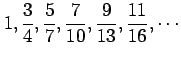 (13)
(13)
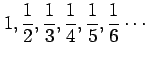
問 4.75 (数列)
次の一般項で定義される数列について
(i)概形を書け.(ii)有限確定,有限不確定, 無限確定,無限不確定
のいずれであるか答えよ.
(1)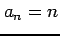 (2)
(2) 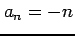 (3)
(3)
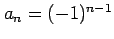
(4)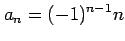 (5)
(5)
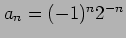
(6)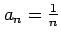 (7)
(7)
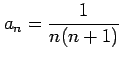
(1)
(4)
(6)
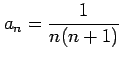
問 4.76 (数列の極限)
極限
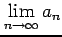 の定義を述べよ.
の定義を述べよ.
問 4.77 (数列の極限)
次の極限値を求めよ.
(1)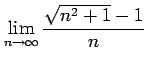 (2)
(2)
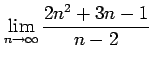 (3)
(3)
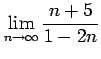 (4)
(4)
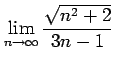
(5)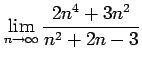 (6)
(6)
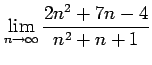 (7)
(7)
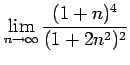 (8)
(8)
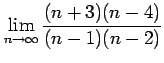
(9)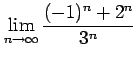 (10)
(10)
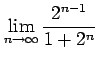 (11)
(11)
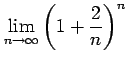 (12)
(12)
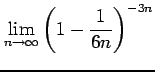
(13)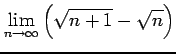 (14)
(14)
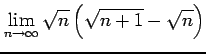 (15)
(15)
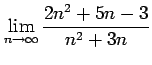
(1)
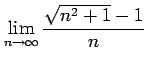 (2)
(2)
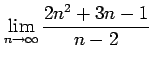 (3)
(3)
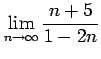 (4)
(4)
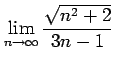
(5)
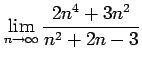 (6)
(6)
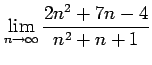 (7)
(7)
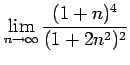 (8)
(8)
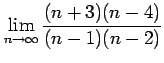
(9)
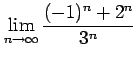 (10)
(10)
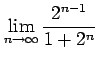 (11)
(11)
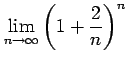 (12)
(12)
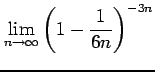
(13)
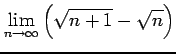 (14)
(14)
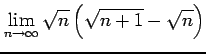 (15)
(15)
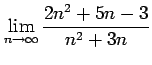
問 4.78 (数列の性質)
数列
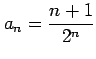 について
次の問いに答えよ.
について
次の問いに答えよ.
(1) 数列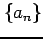 の概形を書け.
(2) 数列
の概形を書け.
(2) 数列 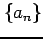 は単調減少であることを示せ.
は単調減少であることを示せ.
(3) 数列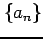 は下に有界であることを示せ.
(4) 極限
は下に有界であることを示せ.
(4) 極限
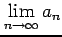 を求めよ.
を求めよ.
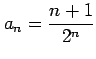 について
次の問いに答えよ.
について
次の問いに答えよ.
(1) 数列
(3) 数列
問 4.79 (等比数列)
等比数列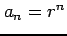
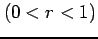 の極限が0になることを証明せよ.
の極限が0になることを証明せよ.
問 4.80 (級数)
級数
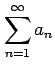 の定義を述べよ.
の定義を述べよ.
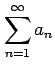 の定義を述べよ.
の定義を述べよ.
問 4.81 (級数)
次の級数について(i) 級数の第 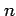 部分和
部分和 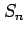 を求めよ.
(ii) 数列
を求めよ.
(ii) 数列 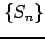 の概形を書け.
(iii) 級数の値を求めよ.
の概形を書け.
(iii) 級数の値を求めよ.
(1)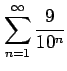 (2)
(2)
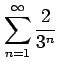 (3)
(3)
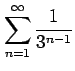 (4)
(4)
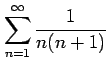 (5)
(5)
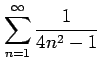 (6)
(6)
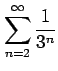
(7)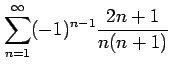
(1)
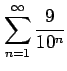 (2)
(2)
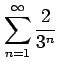 (3)
(3)
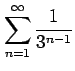 (4)
(4)
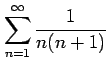 (5)
(5)
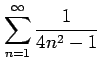 (6)
(6)
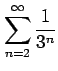
(7)
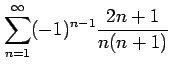
問 4.82 (級数)
次の級数の値を求めよ.
(1)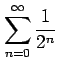 (2)
(2)
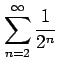 (3)
(3)
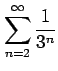 (4)
(4)
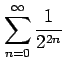 (5)
(5)
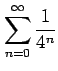 (6)
(6)
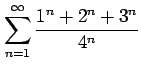
(7)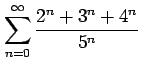 (8)
(8)
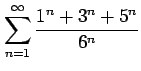 (9)
(9)
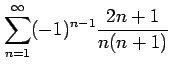
(1)
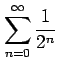 (2)
(2)
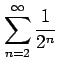 (3)
(3)
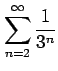 (4)
(4)
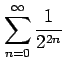 (5)
(5)
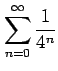 (6)
(6)
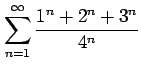
(7)
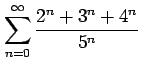 (8)
(8)
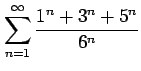 (9)
(9)
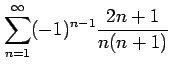
問 4.83 (級数の収束)
次の級数は収束するか発散するか述べよ.
(1)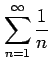 (2)
(2)
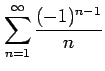 (3)
(3)
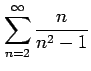 (4)
(4)
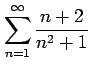 (5)
(5)
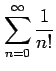 (6)
(6)
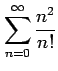
(7)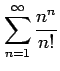 (8)
(8)
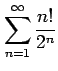 (9)
(9)
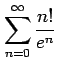 (10)
(10)
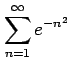 (11)
(11)
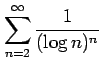 (12)
(12)
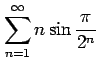
(13)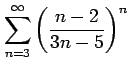 (14)
(14)
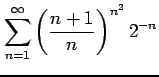 (15)
(15)
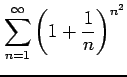 (16)
(16)
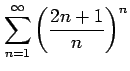
(17)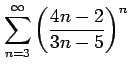
(1)
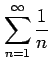 (2)
(2)
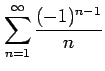 (3)
(3)
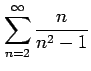 (4)
(4)
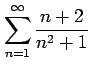 (5)
(5)
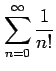 (6)
(6)
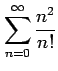
(7)
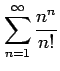 (8)
(8)
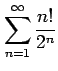 (9)
(9)
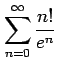 (10)
(10)
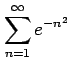 (11)
(11)
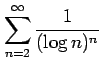 (12)
(12)
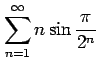
(13)
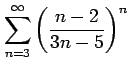 (14)
(14)
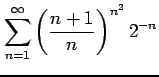 (15)
(15)
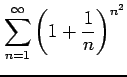 (16)
(16)
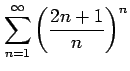
(17)
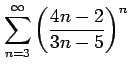
問 4.84 (級数の収束)
次の級数が絶対収束級数か条件収束級数か答えよ.
(1)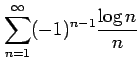 (2)
(2)
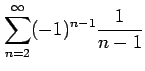 (3)
(3)
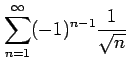 (4)
(4)
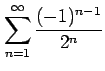
(5)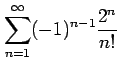 (6)
(6)
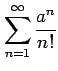 (7)
(7)
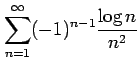 (8)
(8)
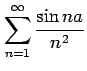 (9)
(9)
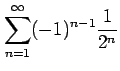
(10)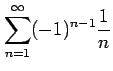 (11)
(11)
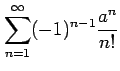
(1)
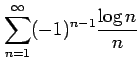 (2)
(2)
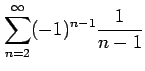 (3)
(3)
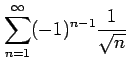 (4)
(4)
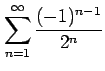
(5)
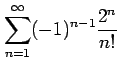 (6)
(6)
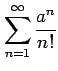 (7)
(7)
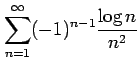 (8)
(8)
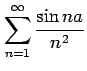 (9)
(9)
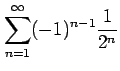
(10)
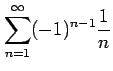 (11)
(11)
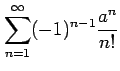
平成19年10月3日