3.8 対数関数の微分
定理 3.20 (対数関数の微分)
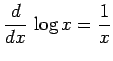 |
問 3.21
これを示せ.
を得る.
(証明)
![]() とおき定義に従い計算すると,
とおき定義に従い計算すると,
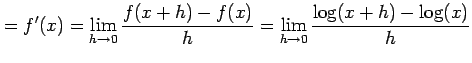 |
||
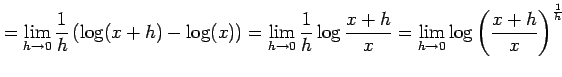 |
||
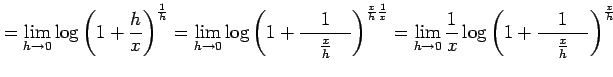 |
||
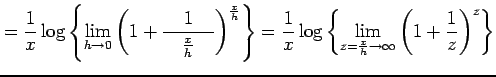 |
||
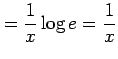 |
を得る.
平成19年10月3日
3.8 対数関数の微分
定理 3.20 (対数関数の微分)
問 3.21 これを示せ.
(証明)
とおき定義に従い計算すると,
を得る.
平成19年10月3日