3.3 導関数の計算
定理 3.9 (微分演算に関する性質)
関数 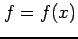 ,
, 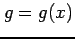 が微分可能なとき,
次の関係が成り立つ:
が微分可能なとき,
次の関係が成り立つ:
- (1)
- (和の微分)
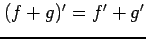 .
.
- (2)
- (微分の線形性)
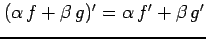 (
(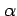 ,
, 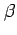 :定数).
:定数).
- (3)
- (積の微分)
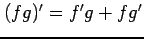 .
.
- (4)
- (商の微分)
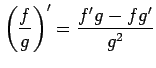 (
(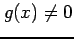 ).
).
- (5)
- (合成関数の微分)
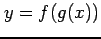 のとき
のとき 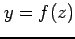 ,
, 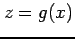 とおけば
とおけば
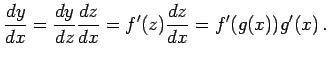
この演算規則をチェインルール(chain rule)と呼ぶ. - (6)
- (逆関数の微分)
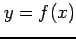 ,
,
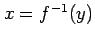 のとき
のとき
例 3.10 (導関数の計算例)
次の関数の導関数を求めよ.
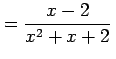 |
||
問 3.11
微分演算に関する性質を示せ.
を得る.
を得る.
を得る.
を得る. ここで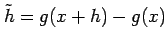 とおくと,
とおくと,
となる.ここで
が成り立つ.よって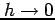 のとき
のとき
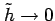 である.
以上より
である.
以上より
を得る.
となる.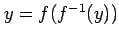 の両辺は
の両辺は 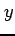 に関する関数である.
両辺を
に関する関数である.
両辺を 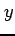 で微分すると
で微分すると
を得る.よって
となる.
(証明)(1)
![]() とおく.
定義に従い計算すると
とおく.
定義に従い計算すると
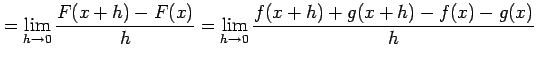 |
||
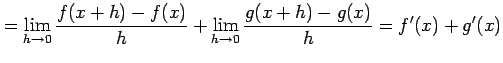 |
を得る.
(2)
![]() とおく.
定義に従い計算すると
とおく.
定義に従い計算すると
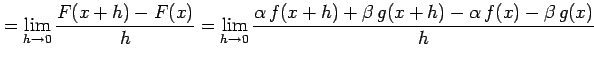 |
||
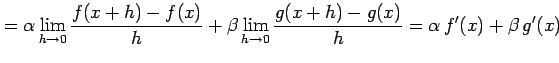 |
を得る.
(3)
![]() とおく.定義に従い計算すると
とおく.定義に従い計算すると
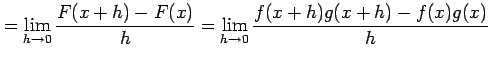 |
||
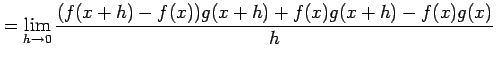 |
||
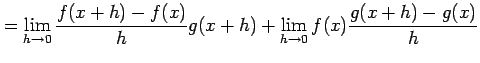 |
||
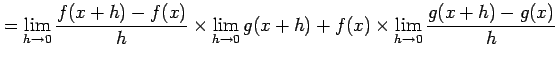 |
||
を得る.
(4)
![]() とおく.定義に従い計算すると,
とおく.定義に従い計算すると,
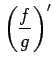 |
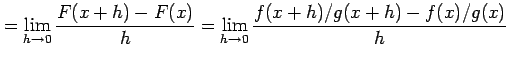 |
|
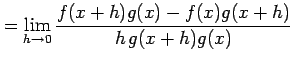 |
||
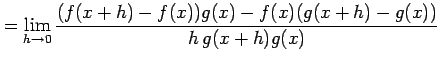 |
||
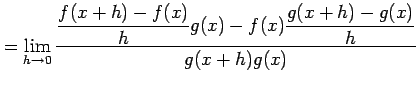 |
||
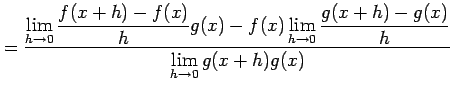 |
||
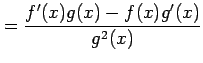 |
を得る.
(5)
![]() とおく.定義に従い計算すると
とおく.定義に従い計算すると
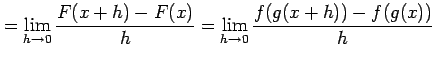 |
||
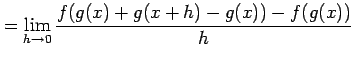 |
||
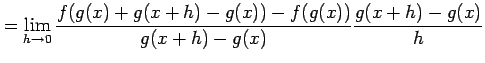 |
を得る. ここで
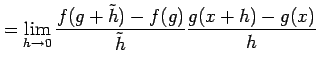 |
||
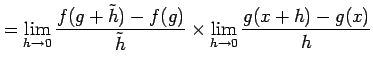 |
となる.ここで
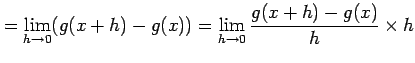 |
||
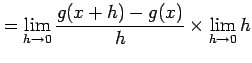 |
||
が成り立つ.よって
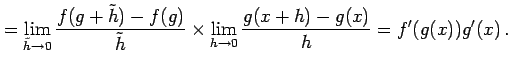 |
を得る.
(6) ![]() ,
,
![]() より
より
となる.
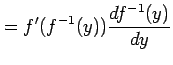 |
||
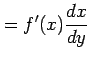 |
||
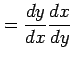 |
を得る.よって
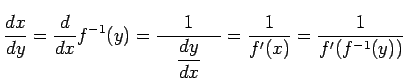 |
となる.
平成19年10月3日