2.36 双曲線関数の極限の計算
例 2.133 (関数の極限の計算例)
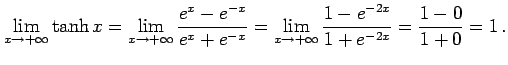 |
||
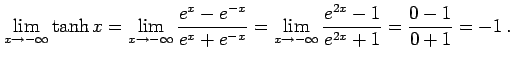 |
例 2.134 (関数の極限の計算例)
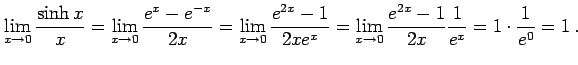 |
例 2.135 (関数の極限の計算例)
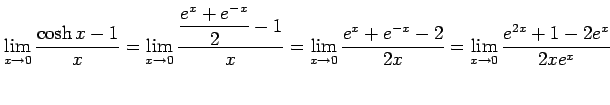 |
||
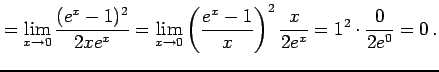 |
例 2.136 (関数の極限の計算例)
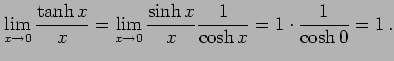 |
平成19年10月3日
2.36 双曲線関数の極限の計算
例 2.133 (関数の極限の計算例)
例 2.134 (関数の極限の計算例)
例 2.135 (関数の極限の計算例)
例 2.136 (関数の極限の計算例)
平成19年10月3日