2.30 関数の収束の速さ比較して極限の計算
例 2.112 (関数の極限の計算例)
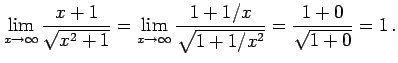 |
例 2.113 (関数の極限の計算例)
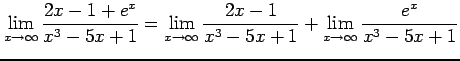 |
||
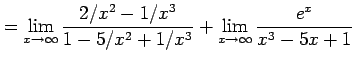 ( ( |
||
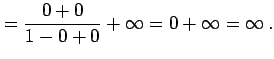 |
例 2.114 (関数の極限の計算例)
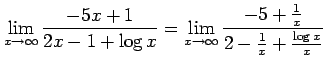 ( ( |
||
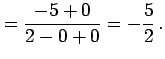 |
例 2.115 (関数の極限の計算例)
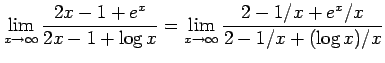 ( (
|
||
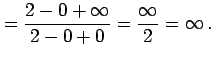 |
平成19年10月3日