1.1 集合
定義 1.1 (集合)
ある一定範囲にある対象物の集まりを1つの全体として考えるとき,
これを集合(set)という.
その範囲内の個々の対象物を元
または要素(element)という.
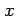 が集合
が集合 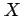 の元であることを
の元であることを
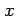 は
は 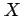 に属する(belong),
または
に属する(belong),
または 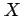 は
は 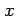 を含む(包含する)(contain)といい,
を含む(包含する)(contain)といい,
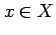 と表記する.その否定を
と表記する.その否定を 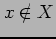 と表記する.
と表記する.
と表記する.
ある元 ![]() が条件
が条件 ![]() をみたすとする.
このとき条件をみたす
をみたすとする.
このとき条件をみたす ![]() 全体の集合を
全体の集合を
と表記する.
例 1.2 (集合の具体例)
| 自然数全体の集合: |
||
| 整数全体の集合: |
||
| 有理数全体の集合: |
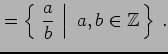 |
|
| 実数全体の集合: |
||
| 複素数全体の集合: |
定義 1.3 (集合の包含関係)
- 元を1つも含まない集合を空集合(empty set)といい,
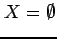 と表記する.
と表記する.
- 集合
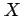 と
と 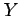 に含まれる元が全て等しいとき
に含まれる元が全て等しいとき 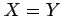 と表記する.
と表記する.
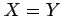 ではないとき
ではないとき 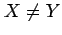 と書く.
と書く.
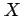 に含まれる全ての元が
に含まれる全ての元が 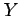 に含まれるとき,
に含まれるとき,
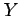 は
は 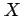 を含む(contain),
または,
を含む(contain),
または,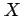 は
は 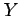 の部分集合(subset)といい,
の部分集合(subset)といい,
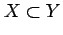 と表記する.
と表記する.
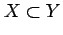 ではないとき
ではないとき
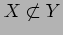 と書く.
と書く.
注意 1.4 (真部分集合)
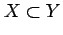 は定義より
は定義より 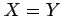 の意味も含む.
の意味も含む.
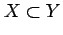 で
で 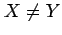 のときは,
のときは,
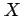 は
は 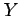 の真部分集合(proper subset)という.
これを
の真部分集合(proper subset)という.
これを
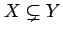 と表記する.
書物によっては部分集合に
と表記する.
書物によっては部分集合に 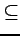 を用い,
真部分集合に
を用い,
真部分集合に 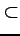 を用いる場合もあるので注意が必要である.
を用いる場合もあるので注意が必要である.
例 1.5 (包含関係の具体例)
例 1.6 (包含関係の具体例)
のとき
が成立する.
のとき
が成立する.
平成19年10月3日