2.20 逆三角関数
三角関数の逆関数を
逆三角関数(inverse trigonometric function)と呼び,
![]() ,
, ![]() ,
, ![]() の逆関数をそれぞれ
の逆関数をそれぞれ
と書き表す. 読み方は上から sine inverse, cosine inverse, tangent inverse または arc sine, arc cosine, arc tangent である. 逆三角関数は多価関数となる. 任意の
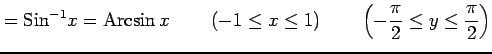 |
||
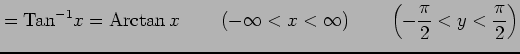 |
と書く.
問 2.58 (逆三角関数のグラフ)
逆三角関数の概形を書け.
例 2.59 (逆三角関数の値)
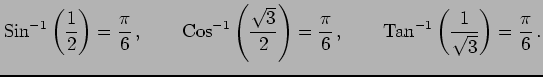 |
問 2.60 (逆三角関数の値)
次の値を求めよ.
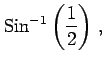 |
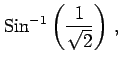 |
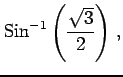 |
||||||||
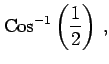 |
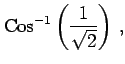 |
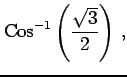 |
||||||||
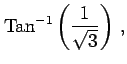 |
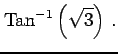 |
平成19年10月3日