6.26 演習 〜 広義積分
問 6.124 (広義積分)
次の積分を求めよ.
(1)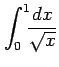 (2)
(2)
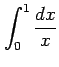 (3)
(3)
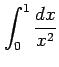 (4)
(4)
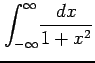 (5)
(5)
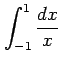
(6)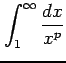 (ただし,
(ただし,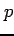 は正の実数)
(7)
は正の実数)
(7)
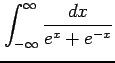 (8)
(8)
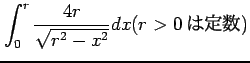
(9)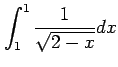 (10)
(10)
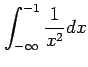 (11)
(11)
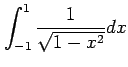 (12)
(12)
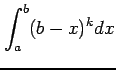
(13)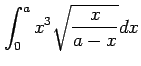 (14)
(14)
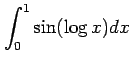 (15)
(15)
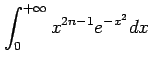 (16)
(16)
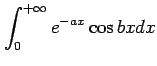
(17)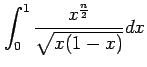
(1)
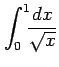 (2)
(2)
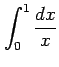 (3)
(3)
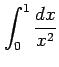 (4)
(4)
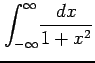 (5)
(5)
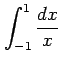
(6)
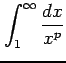 (ただし,
(ただし,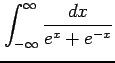 (8)
(8)
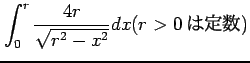
(9)
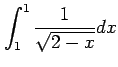 (10)
(10)
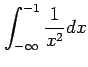 (11)
(11)
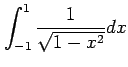 (12)
(12)
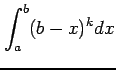
(13)
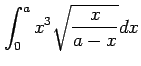 (14)
(14)
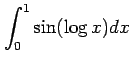 (15)
(15)
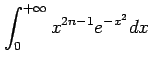 (16)
(16)
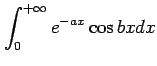
(17)
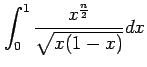
平成19年10月3日