6.11 演習 〜 有理式,根号,三角関数の積分
問 6.55 (有理式の積分)
次の不定積分を求めよ.
(1)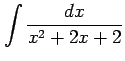 (2)
(2)
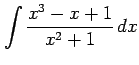 (3)
(3)
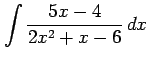 (4)
(4)
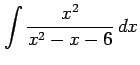
(5)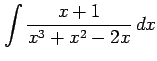 (6)
(6)
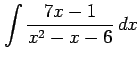 (7)
(7)
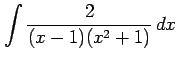 (8)
(8)
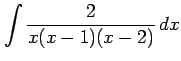
(9)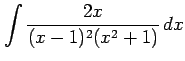 (10)
(10)
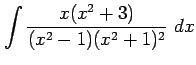 (11)
(11)
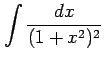 (12)
(12)
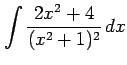
(13)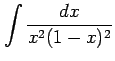 (14)
(14)
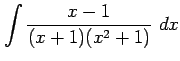 (15)
(15)
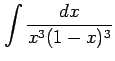
(1)
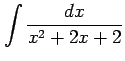 (2)
(2)
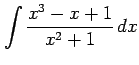 (3)
(3)
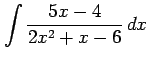 (4)
(4)
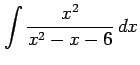
(5)
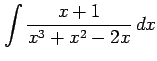 (6)
(6)
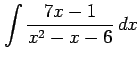 (7)
(7)
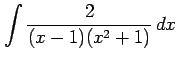 (8)
(8)
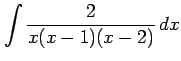
(9)
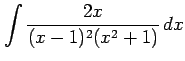 (10)
(10)
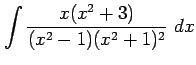 (11)
(11)
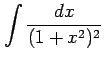 (12)
(12)
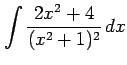
(13)
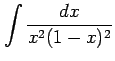 (14)
(14)
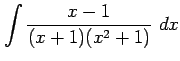 (15)
(15)
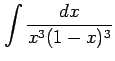
問 6.56 (根号を含む積分)
次の不定積分を求めよ.
(1)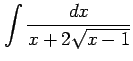 (2)
(2)
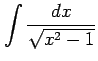 (3)
(3)
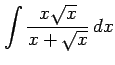 (4)
(4)
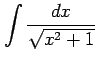 (5)
(5)
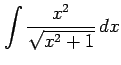
(6)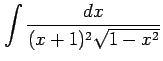 (7)
(7)
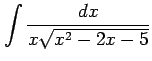
(1)
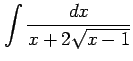 (2)
(2)
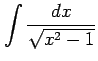 (3)
(3)
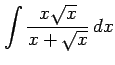 (4)
(4)
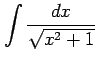 (5)
(5)
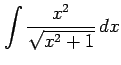
(6)
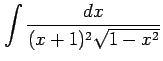 (7)
(7)
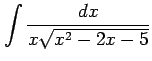
問 6.57 (三角関数を含む有理式の積分)
次の不定積分を求めよ.
(1)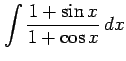 (2)
(2)
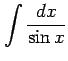 (3)
(3)
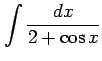 (4)
(4)
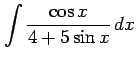 (5)
(5)
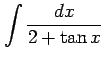
(6)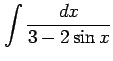 (7)
(7)
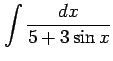
(1)
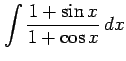 (2)
(2)
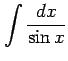 (3)
(3)
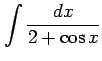 (4)
(4)
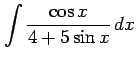 (5)
(5)
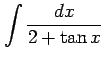
(6)
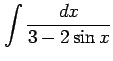 (7)
(7)
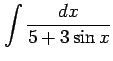
平成19年10月3日