5.13 割り算によるテイラー級数の計算
例 5.29 (テイラー級数の計算例)
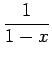 |
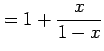 |
|
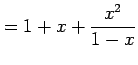 |
||
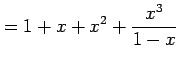 |
||
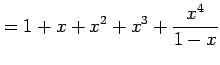 |
||
例 5.30 (テイラー級数の計算例)
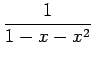 |
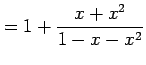 |
|
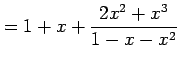 |
||
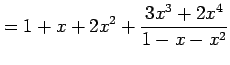 |
||
例 5.31 (テイラー級数の計算例)
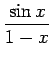 |
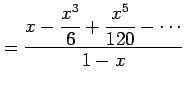 |
|
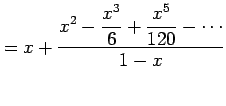 |
||
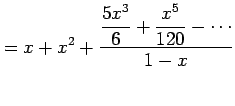 |
||
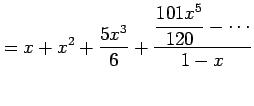 |
||
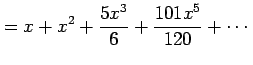 |
例 5.32 (テイラー級数の計算例)
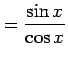 |
||
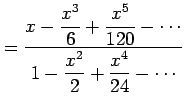 |
||
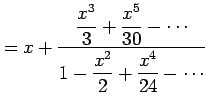 |
||
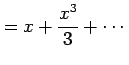 |
平成19年10月3日