4.20
 における回転
における回転
例 4.86 (
 の回転)
直交変換
の回転)
直交変換
を考える. この写像は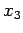 軸を中心に
軸を中心に 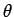 回転を表す.
回転を表す.
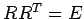 より
より 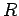 は直交行列である.
は直交行列である.
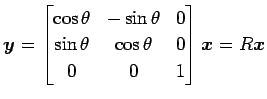 |
を考える. この写像は
例 4.87 (
 の回転)
の回転)
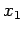 軸まわりの回転は
軸まわりの回転は
と表され,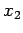 軸まわりの回転は
軸まわりの回転は
と表され,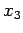 軸まわりの回転は
軸まわりの回転は
と表される.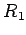 ,
, 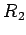 ,
, 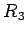 は直交行列である.
は直交行列である.
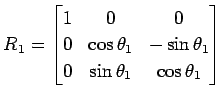 |
と表され,
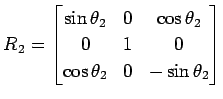 |
と表され,
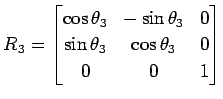 |
と表される.
注意 4.88 (
 の回転)
の回転)
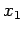 軸まわりに回転し,その後
軸まわりに回転し,その後 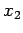 軸まわりに回転させるとき,
表現行列は
軸まわりに回転させるとき,
表現行列は 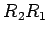 である.これもまた直交行列である.
同様に
である.これもまた直交行列である.
同様に 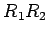 ,
, 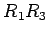 ,
,  もまた回転を表す.
ただし,
もまた回転を表す.
ただし,
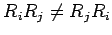 であることに注意.
回転させる順番が異なれば違う回転を表す.
であることに注意.
回転させる順番が異なれば違う回転を表す.
問 4.89 (
 の回転)
原点を通り方向ベクトルが
の回転)
原点を通り方向ベクトルが
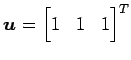 の直線を軸とする回転を考える.
この回転変換の表現行列を求めよ.
の直線を軸とする回転を考える.
この回転変換の表現行列を求めよ.
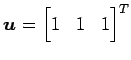 の直線を軸とする回転を考える.
この回転変換の表現行列を求めよ.
の直線を軸とする回転を考える.
この回転変換の表現行列を求めよ.
Kondo Koichi

平成18年1月17日