4.11 恒等変換の表現行列
定理 4.53 (恒等変換の表現行列)
恒等変換 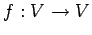 の表現行列は単位行列である.
の表現行列は単位行列である.
をみたす.よって
となるので,表現行列は単位行列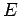 となる.
となる.
(証明)
![]() の基底を
の基底を
![]() とする.
このとき
とする.
このとき ![]() は恒等変換であるから,
は恒等変換であるから,
をみたす.よって
となるので,表現行列は単位行列
Kondo Koichi

平成18年1月17日