4.8 線形写像の像と核
定義 4.40 (像)
線形写像 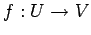 に対して集合
に対して集合
を の像(image)という.
の像(image)という.
を
定義 4.41 (核)
線形写像 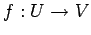 に対して集合
に対して集合
を の核(kernel)という.
の核(kernel)という.
を
定理 4.42 (像と部分空間)
線形写像 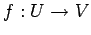 の像
の像
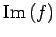 は
は
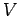 の部分空間である.
の部分空間である.
が成り立つ. つまり,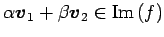 である.
任意のベクトル
である.
任意のベクトル
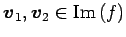 と
任意のスカラー
と
任意のスカラー
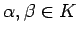 に対して,
に対して,
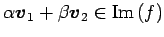 が成り立つので,
が成り立つので,
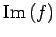 は
は 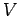 の部分空間である.
の部分空間である.
(証明)
像
![]() のベクトル
のベクトル
![]() に対して
に対して
![]() ,
,
![]() を
みたすベクトル
を
みたすベクトル
![]() をおく.
このとき,
をおく.
このとき,
が成り立つ. つまり,
定理 4.43 (核と部分空間)
線形写像 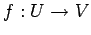 の
核
の
核
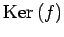 は
は 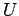 の部分空間である.
の部分空間である.
となる. つまり,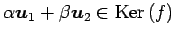 である.
任意のベクトル
である.
任意のベクトル
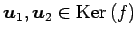 と
任意のスカラー
と
任意のスカラー
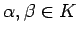 に対して,
に対して,
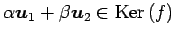 が成り立つので,
が成り立つので,
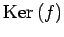 は
は 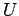 の部分空間である.
の部分空間である.
(証明)
核
![]() のベクトル
のベクトル
![]() は
は
![]() ,
,
![]() をみたす.
このとき,
をみたす.
このとき,
となる. つまり,
Kondo Koichi

平成18年1月17日