3.47 正規直交基底で生成される部分空間の直交補空間
例 3.190 (直交補空間の具体例)
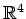 において,
において,
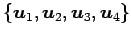 を直交基底とする.
このとき
を直交基底とする.
このとき
が成り立つ. ここで
とおくと,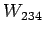 は
は
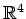 における
における 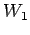 の直交補空間となる.
なぜなら任意のベクトル
の直交補空間となる.
なぜなら任意のベクトル
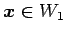 ,
,
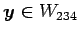 に対して
に対して
が成り立ち,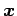 と
と 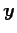 は直交するからである.
よって
は直交するからである.
よって
であり,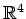 は
は 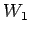 とその直交補空間
とその直交補空間 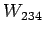 に
よって直和分解される.
同様に
に
よって直和分解される.
同様に
と部分空間とのその直交補空間とで直和分解される. ただし,
とおく.
が成り立つ. ここで
とおくと,
が成り立ち,
であり,
と部分空間とのその直交補空間とで直和分解される. ただし,
とおく.
例 3.191 (直交補空間の具体例)
直交基底
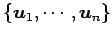 で
生成されるベクトル空間
で
生成されるベクトル空間
を考える.このとき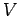 は直和分解されて
は直和分解されて
と表される.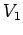 は
は 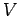 における
における 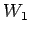 の直交補空間である.
さらに
の直交補空間である.
さらに 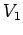 を直和分解して
を直和分解して
と表される.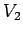 は
は 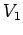 における
における 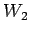 の直交補空間である.
同様に繰り返して直交補空間で直和分解が可能である:
の直交補空間である.
同様に繰り返して直交補空間で直和分解が可能である:
を考える.このとき
と表される.
と表される.
Kondo Koichi

平成18年1月17日