3.45 解空間の直交補空間
例 3.186 (直交補空間の具体例)
 の部分空間
の部分空間
の基底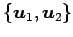 に
それぞれ直交するベクトルのひとつは
に
それぞれ直交するベクトルのひとつは
である. このベクトルにより生成される部分空間
は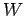 の直交補空間
の直交補空間 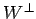 となる.
なぜなら,任意のベクトル
となる.
なぜなら,任意のベクトル
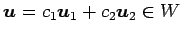 ,
,
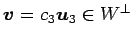 に対して
に対して
が成り立つからである. また,
が成り立つ.
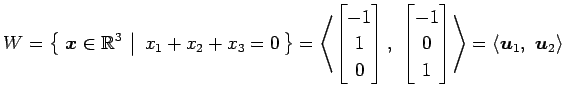 |
の基底
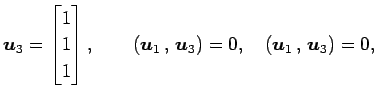 |
である. このベクトルにより生成される部分空間
は
が成り立つからである. また,
が成り立つ.
例 3.187 (直交補空間の具体例)
方程式
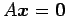 の解空間
の解空間
の における直交補空間
における直交補空間 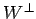 を求める.
行列
を求める.
行列  を簡約化すると
を簡約化すると
となるから,解空間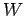 は
は
と表される.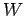 の任意のベクトル
の任意のベクトル
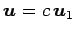 (
(
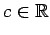 )
と直交するベクトル
)
と直交するベクトル
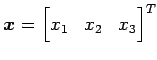 を求める.
を求める.
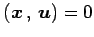 より,
より,
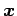 の成分は方程式
の成分は方程式
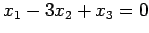 を
みたさなければならない.
よって,
を
みたさなければならない.
よって,
となる. これは方程式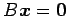 の解空間であるから,
行列
の解空間であるから,
行列 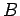 を簡約化して
を簡約化して
より,
と得られる. また,
が成り立ち,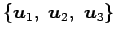 は
は
 の基底となる.
の基底となる.
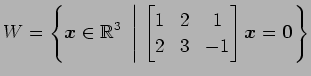 |
の
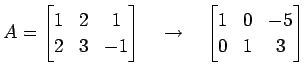 |
となるから,解空間
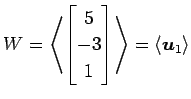 |
と表される.
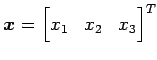 を求める.
を求める.
となる. これは方程式
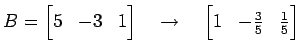 |
より,
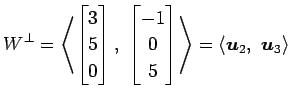 |
と得られる. また,
が成り立ち,
Kondo Koichi

平成18年1月17日