3.34 座標
定義 3.129 (座標)
ベクトル空間 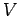 と
その基底を
と
その基底を
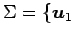 ,
,
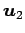 ,
,  ,
,
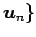 とする.
このとき
とする.
このとき 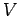 の任意の元
の任意の元 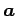 は
は
と表せる. 線形結合の係数の組
を基底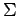 における座標(coordinate)という.
また,誤解がないときは単に
における座標(coordinate)という.
また,誤解がないときは単に
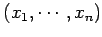 と表記する.
と表記する.
![$\displaystyle \vec{a}= x_{1}\vec{u}_{1}+ x_{2}\vec{u}_{2}+ \cdots+ x_{n}\vec{u}...
...t)\begin{bmatrix}x_1 \\ [-1ex] x_2 \\ [-1ex] \vdots \\ [-1ex] x_n \end{bmatrix}$](img1463.png) |
と表せる. 線形結合の係数の組
を基底
注意 3.130 (列行列の成分)
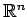 の
標準基底
の
標準基底
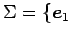 ,
,
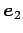 ,
,  ,
,
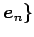 における任意のベクトル
における任意のベクトル 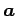 の座標を
の座標を
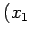 ,
, 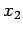 ,
,  ,
,
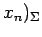 とする.
このとき,
とする.
このとき,
と書ける. 列ベクトル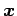 の成分の組
の成分の組
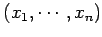 は
標準基底における座標と見なされる.
は
標準基底における座標と見なされる.
![$\displaystyle \vec{a}= x_{1}\vec{e}_{1}+ x_{2}\vec{e}_{2}+ \cdots+ x_{n}\vec{e}...
...x}x_{1} \\ [-1ex] x_{2} \\ [-1ex] \vdots \\ [-1ex] x_{n} \end{bmatrix}= \vec{x}$](img1473.png) |
と書ける. 列ベクトル
例 3.131 (座標の具体例)
 の点
の点 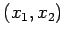 の位置ベクトルを
の位置ベクトルを 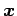 とする.
とする.
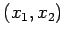 は標準基底
は標準基底
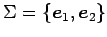 における
座標
における
座標
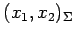 とみなせるから,
とみなせるから,
と表される. 次に基底
における座標を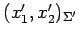 とすると,
とすると,
と書ける. このとき
が成り立つ. よって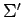 における座標は
における座標は
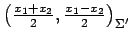 となる.
例えば点
となる.
例えば点
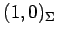 ,
,
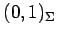 ,
,
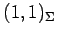 は
は
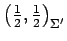 ,
,
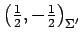 ,
,
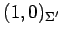 となる.
となる.
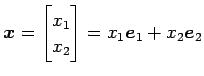 |
と表される. 次に基底
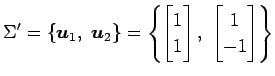 |
における座標を
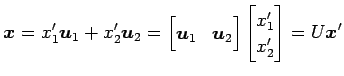 |
と書ける. このとき
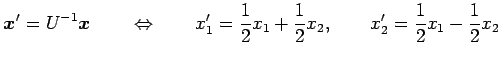 |
が成り立つ. よって
例 3.132 (座標の具体例)
![$ \mathbb{R}[x]_n$](img373.png) のベクトルは多項式
のベクトルは多項式
である.任意の の基底
の基底
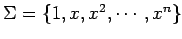 における
座標は
における
座標は
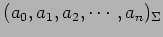 である.
である.
である.任意の
Kondo Koichi

平成18年1月17日