1.4 体
ある集合の元に対して四則演算が定義され, その集合内で閉じているとき, その集合を体と呼ぶ. 正確には次のように定義される.
定義 1.15 (体)
集合 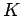 の任意の 2 つの元
の任意の 2 つの元 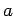 ,
, 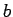 に対して,
加法
に対して,
加法 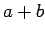 と乗法
と乗法 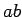 が定義されているとする.
が定義されているとする.
| (1) |
|
(和の結合則) |
| (2) |
|
(零元 0 の存在) |
| (3) |
|
(和の逆元 |
| (4) | |
(和の交換則) |
| (5) |
|
(積の結合則) |
| (6) |
|
(分配則) |
| (7) | |
(積の交換則) |
| (8) |
|
(単位元 |
| (9) |
|
(積の逆元 |
- 条件(1)-(3) を満たすとき,
集合
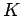 を群(group)と呼ぶ.
を群(group)と呼ぶ.
- 条件(1)-(4) を満たすとき,
集合
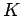 を可換群(commutative group)
またはアーベル群(Abel group)と呼ぶ.
を可換群(commutative group)
またはアーベル群(Abel group)と呼ぶ.
- 条件(1)-(6) を満たすとき,
集合
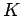 を環(ring)と呼ぶ.
を環(ring)と呼ぶ.
- 条件(1)-(7) を満たすとき,
集合
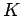 を可換環(commutative ring)と呼ぶ.
を可換環(commutative ring)と呼ぶ.
- 条件(1)-(9) を満たすとき,
集合
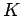 を体(field)と呼ぶ.
ただし,
条件(7)を満たさない体を
非可換体(noncommutative field)と呼ぶ.
を体(field)と呼ぶ.
ただし,
条件(7)を満たさない体を
非可換体(noncommutative field)と呼ぶ.
例 1.16 (体の具体例)
数の集合
を考える.
を考える.
- 自然数全体の集合
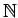 を考える.
を考える.
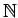 は加法,乗法ともに群をなさない.
なぜなら,和の逆元
は加法,乗法ともに群をなさない.
なぜなら,和の逆元 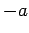 ,積の逆元
,積の逆元 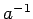 は自然数の
範囲内で存在しないからである.
は自然数の
範囲内で存在しないからである.
- 整数全体の集合
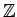 を考える.
を考える.
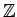 は可換環である.
積の逆元が存在しないので体とはならないことに注意する.
は可換環である.
積の逆元が存在しないので体とはならないことに注意する.
- 有理数全体の集合
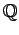 を考える.
を考える.
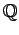 は体である.
は体である.
- 実数全体の集合
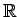 を考える.
を考える.
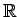 は体である.
は体である.
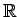 を実数体(real number field)と呼ぶ.
を実数体(real number field)と呼ぶ.
- 複素数全体の集合
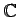 を考える.
を考える.
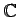 は体である.
は体である.
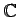 を複素数体(complex number field)と呼ぶ.
を複素数体(complex number field)と呼ぶ.
例 1.17 (体の具体例)
- 0 でない実数全体の集合
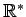 は
乗法に関して可換群となる.
(∵)
積
は
乗法に関して可換群となる.
(∵)
積 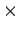 を和
を和 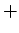 に置き換えて考える.
条件(5), (8), (9), (7)は条件(1), (2), (3), (4)とみなせる.
に置き換えて考える.
条件(5), (8), (9), (7)は条件(1), (2), (3), (4)とみなせる.
- 行列の集合
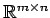 は
加法に関して可換群となる.
(∵)
(1)
は
加法に関して可換群となる.
(∵)
(1)
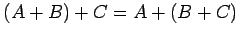 . (2)
. (2) 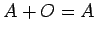 . (3)
. (3) 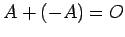 . (4)
. (4) 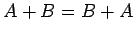 .
.
- 正方行列の集合
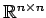 は
加法と乗法に関して環となる.
(∵)
条件(1)-(4)と(5)
は
加法と乗法に関して環となる.
(∵)
条件(1)-(4)と(5)
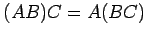 .
(6)
.
(6)
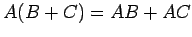 .
(注意) 単位元は単位行列
.
(注意) 単位元は単位行列 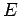 である.
である.
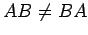 であるから可換環ではない.
であるから可換環ではない.
- 正則な
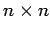 型行列の集合
型行列の集合 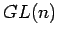 は非可換体となる.
(∵)
(8)
は非可換体となる.
(∵)
(8) 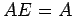 .
(9)
.
(9) 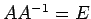 .
(7)
.
(7) 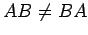 .
.
Kondo Koichi

平成18年1月17日