3.25 基底
定義 3.92 (基底)
ベクトル空間 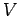 が 1 次独立なベトクル
が 1 次独立なベトクル
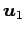 ,
,
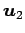 ,
,  ,
,
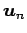 により生成される空間
により生成される空間
として表されるとき, ベクトルの組
を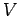 の基底(basis)という.
の基底(basis)という.
として表されるとき, ベクトルの組
を
例 3.93 (基底の具体例)
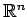 は
基本ベクトル
は
基本ベクトル
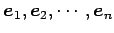 を用いて
を用いて
と表される. また,基本ベクトル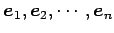 は
1 次独立であるから,
は
1 次独立であるから,
は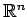 の基底である.
これを
の基底である.
これを
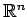 の標準基底(standard basis)という.
の標準基底(standard basis)という.
と表される. また,基本ベクトル
は
注意 3.94 (基底の取り方の非一意性)
基底の取り方は一意ではない.
例 3.95 (基底の具体例)
 の基底を考える.
の基底を考える.
 は標準基底
は標準基底
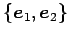 をもち,
をもち,
と表される. 他の基底を考える. 例えば,
は基底となり得るか調べる. まず,
であるから,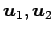 は 1 次独立である.
次に,
は 1 次独立である.
次に,
となるか調べる. すなわち の任意のベクトル
の任意のベクトル 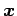 に対して
に対して
をみたす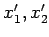 が一意に定まるか調べる.
この式を書き換えると
が一意に定まるか調べる.
この式を書き換えると
となる. これは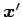 についての非同次連立方程式
についての非同次連立方程式
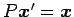 である.
である.
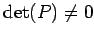 より
より 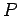 は正則であるから
は正則であるから
となる.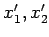 は任意の
は任意の 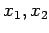 に対して一意に定まる.
よって,
に対して一意に定まる.
よって,
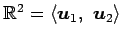 が成り立つ.
以上より
が成り立つ.
以上より
は の基底である.
の基底である.
と表される. 他の基底を考える. 例えば,
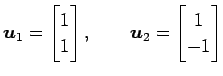 |
は基底となり得るか調べる. まず,
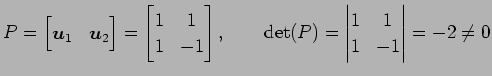 |
であるから,
となるか調べる. すなわち
をみたす
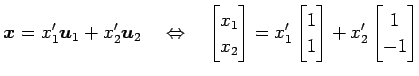 |
||
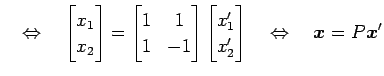 |
となる. これは
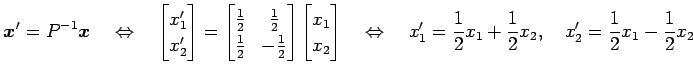 |
となる.
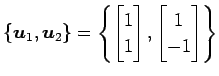 |
は
Kondo Koichi

平成18年1月17日