3.15 ベトクルの 1 次独立の性質 〜 その 2
定理 3.63 (ベトクルの 1 次独立の性質)
ベクトル 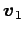 ,
, 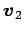 ,
,  ,
,
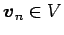 の
各ベクトルが
の
各ベクトルが
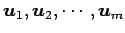 の
1 次結合で表され,
かつ,
の
1 次結合で表され,
かつ,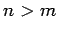 であるとき,
であるとき,
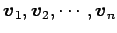 は 1 次従属である.
は 1 次従属である.
と書ける.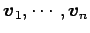 の 1 次関係は
の 1 次関係は
となる. ここで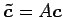 とおいた.
このとき
とおいた.
このとき
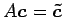 を
を
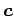 に関する方程式であると考える.
に関する方程式であると考える.
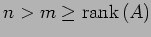 より
より
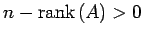 となるので,
方程式の解は
となるので,
方程式の解は 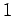 個以上の任意定数を含む.
よって非自明解をもつので,
個以上の任意定数を含む.
よって非自明解をもつので,
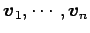 は
非自明な 1 次関係の係数
は
非自明な 1 次関係の係数 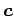 をもつ.
をもつ.
(証明)
ベクトル
![]() は
は
![]() の 1 次結合で表されるので,
の 1 次結合で表されるので,
 |
と書ける.
 |
||
となる. ここで
例 3.64 (ベトクルの 1 次独立の性質)
ベクトル
は基本ベクトル ,
, 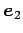 を用いると
を用いると
か書けるので,
となる.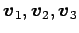 の 1 次関係は
の 1 次関係は
となる. ここで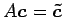 とおいた.
これは
とおいた.
これは 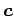 に関する方程式となみせる.
(☆)は
に関する方程式となみせる.
(☆)は 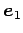 ,
, 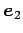 の 1 次関係ともみなせる.
の 1 次関係ともみなせる.
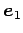 ,
, 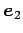 は 1 次独立であるから,
自明な係数
は 1 次独立であるから,
自明な係数
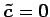 のみをもつ.
よって
のみをもつ.
よって
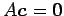 となる.
となる.
 より解の任意定数の個数は
より解の任意定数の個数は
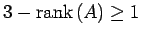 となる.
以上より
となる.
以上より 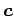 は非自明な解となるから,
は非自明な解となるから,
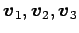 は非自明な係数
は非自明な係数 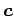 をもつ.
よって,
をもつ.
よって,
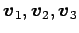 は 1 次従属である.
は 1 次従属である.
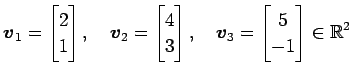 |
は基本ベクトル
か書けるので,
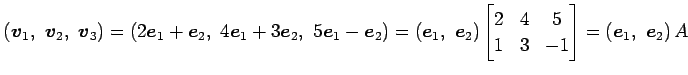 |
となる.
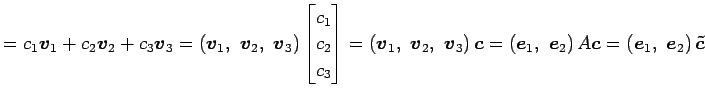 |
となる. ここで
注意 3.65 (ベトクルの 1 次独立の性質)
ベクトル空間
 の
の
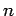 個のベクトル
個のベクトル 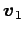 ,
, 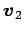 ,
, 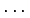 ,
, 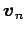 は,
は,
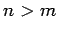 のとき 1 次従属である.
のとき 1 次従属である.
定理 3.66 (ベトクルの 1 次独立の性質)
ベクトル 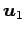 ,
, 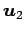 ,
, 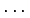 ,
,
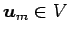 と
行列
と
行列
![$ A=[a_{ij}]_{m\times n}$](img805.png) に対して,
次の条件(i), (ii)が成り立つとき,
に対して,
次の条件(i), (ii)が成り立つとき,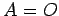 が成り立つ.
が成り立つ.
より,
となる. それぞれが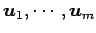 の
1 次関係である.
の
1 次関係である.
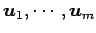 は 1 次独立であるので,
係数は自明なもののみに限る.
よって
は 1 次独立であるので,
係数は自明なもののみに限る.
よって 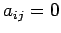 となり,
となり,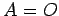 を得る.
を得る.
- (i).
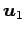 ,
, 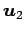 ,
,  ,
, 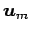 は 1 次独立.
は 1 次独立.
- (ii).
-
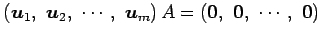 .
.
(証明)
より,
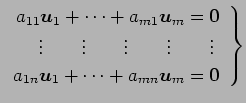 |
となる. それぞれが
注意 3.67 ( 1 次関係)
特に
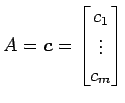 とおく.
このとき
とおく.
このとき
となり,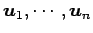 の 1 次関係を得る.
の 1 次関係を得る.
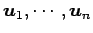 が 1 次独立であれば,
が 1 次独立であれば,
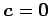 となる.
となる.
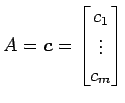 とおく.
このとき
とおく.
このとき
 |
となり,
定理 3.68 (ベトクルの 1 次独立の性質)
ベクトル
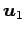 ,
, 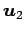 ,
,  ,
,
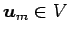 が 1 次独立であれば,
が 1 次独立であれば,
のとき,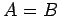 が成立する.
が成立する.
のとき,
(証明)
例 3.69 (ベトクルの 1 次独立の性質)
ベクトル
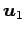 ,
, 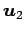 ,
, 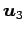 ,
,
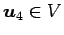 は 1 次独立であり,
ベクトル
は 1 次独立であり,
ベクトル 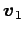 ,
, 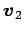 ,
, 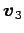 ,
,
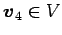 は
は
により与えられているとする. このとき,
となる.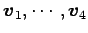 の 1 次関係は
の 1 次関係は
である. ここで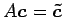 とおいた.
これは
とおいた.
これは
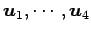 の 1 次関係ともみなせる.
の 1 次関係ともみなせる.
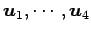 は 1 次独立であるから,
自明な係数
は 1 次独立であるから,
自明な係数
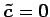 のみをもつ.
よって
のみをもつ.
よって
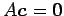 が成り立つ.
が成り立つ.
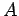 を簡約化すると
を簡約化すると 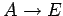 であり,
であり,
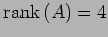 より,
解は自明な解
より,
解は自明な解
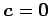 に限る.
以上より
に限る.
以上より
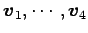 は自明な係数
は自明な係数
 のみをもつので,1 次独立である.
のみをもつので,1 次独立である.
により与えられているとする. このとき,
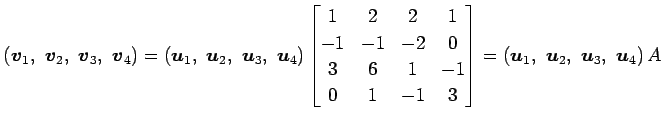 |
となる.
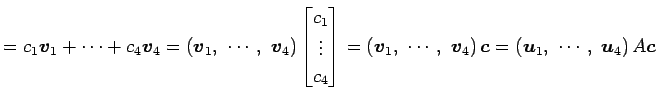 |
||
である. ここで
例 3.70 (ベトクルの 1 次独立の性質)
ベクトル
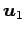 ,
, 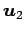 ,
, 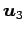 ,
,
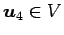 は 1 次独立であり,
ベクトル
は 1 次独立であり,
ベクトル 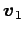 ,
, 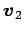 ,
, 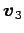 ,
,
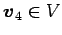 は
は
により与えられているとする. このとき,
となる.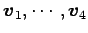 の 1 次関係は
の 1 次関係は
である. ここで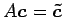 とおいた.
これは
とおいた.
これは
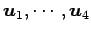 の 1 次関係ともみなせる.
の 1 次関係ともみなせる.
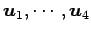 は 1 次独立であるから,
自明な係数
は 1 次独立であるから,
自明な係数
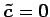 のみをもつ.
よって
のみをもつ.
よって
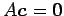 が成り立つ.
が成り立つ.
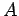 を簡約化すると
を簡約化すると
であり,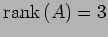 より,
解は非自明な解
より,
解は非自明な解
をもつ. よって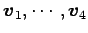 の 1 次関係は
の 1 次関係は
となる. 非自明な 1 次関係であるから,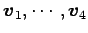 は 1 次従属である.
は 1 次従属である.
により与えられているとする. このとき,
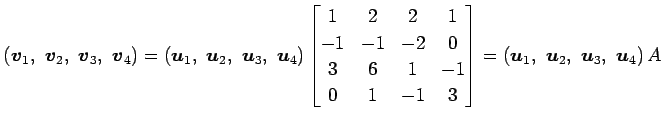 |
となる.
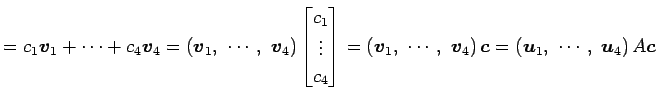 |
||
である. ここで
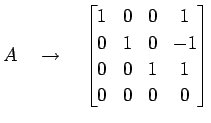 |
であり,
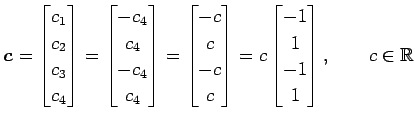 |
をもつ. よって
となる. 非自明な 1 次関係であるから,
Kondo Koichi

平成18年1月17日