3.12 正規直交系は 1 次独立
定理 3.54 (直交系の 1 次独立性)
内積空間 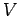 において,
ベクトル
において,
ベクトル
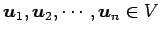 が直交系であるとき,
が直交系であるとき,
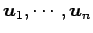 は 1 次独立である.
は 1 次独立である.
の両辺と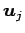 との内積をとると
との内積をとると
となる.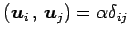 (
(
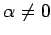 ) より
) より
を得る.すべての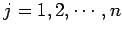 に対して
同様に成り立つので
に対して
同様に成り立つので
となる. 自明な 1 次関係のみであるから, ベクトル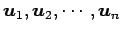 は
1 次独立である.
は
1 次独立である.
(証明) 1 次関係
の両辺と
となる.
を得る.すべての
となる. 自明な 1 次関係のみであるから, ベクトル
Kondo Koichi

平成18年1月17日