3.7
![$ \mathbb{R}[x]_n$](img373.png) の部分空間
の部分空間
例 3.35 (多項式からなる部分空間の具体例)
ベクトル空間
の部分集合
は![$ \mathbb{R}[x]_3$](img554.png) の部分空間ではない.
の部分空間ではない.
の部分集合
は
(証明)
(i)
![]() の零ベクトルは
の零ベクトルは ![]() である.
である.
![]() ,
, ![]() となるから,
となるから,
![]() である.
(ii)
である.
(ii)
![]() とする.
すなわち
とする.
すなわち
![]() ,
,
![]() をみたすとする.
このとき
をみたすとする.
このとき
![]() が成り立つ.
よって
が成り立つ.
よって ![]() となる.
(iii)
となる.
(iii)
![]() ,
,
![]() とする.
任意の
とする.
任意の
![]() に対して
に対して
![]() が成り立つ.よって
が成り立つ.よって
![]() となる.
(i), (ii), (iii)より,
となる.
(i), (ii), (iii)より,
![]() は
は
![]() の部分空間である.
の部分空間である.
例 3.36 (多項式からなる部分空間の具体例)
ベクトル空間
![$ \mathbb{R}[x]_3$](img554.png) の部分集合
の部分集合
は![$ \mathbb{R}[x]_3$](img554.png) の部分空間ではない.
なぜなら,
の部分空間ではない.
なぜなら,
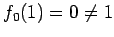 となるから,
となるから,
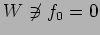 である.
よって
である.
よって 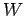 は
は
![$ \mathbb{R}[x]_3$](img554.png) の部分空間ではない.
の部分空間ではない.
は
例 3.37 (多項式からなる部分空間の具体例)
ベクトル空間
![$ \mathbb{R}[x]_3$](img554.png) の部分集合
の部分集合
は![$ \mathbb{R}[x]_3$](img554.png) の部分空間である.
の部分空間である.
となる.任意の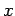 について成り立つので,
について成り立つので,
である.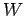 の任意の元は
の任意の元は 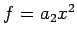 と表される.
(i)
と表される.
(i) 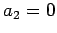 のとき
のとき
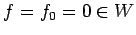 .
(ii)
.
(ii) 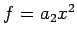 ,
, 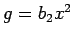
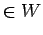 に対して
に対して
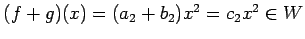 .
(iii)
.
(iii)
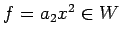 ,
,
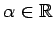 に対して
に対して
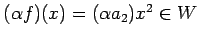 .
(i), (ii), (iii)より
.
(i), (ii), (iii)より
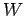 は
は
![$ \mathbb{R}[x]_3$](img554.png) の部分空間である.
の部分空間である.
は
(証明)
![]() の任意の元は
の任意の元は
![]() である.
このとき
である.
このとき ![]() より
より
となる.任意の
である.
Kondo Koichi

平成18年1月17日