1.1 集合
定義 1.1 (集合)
ある一定範囲にある対象物の集まりを1つの全体として考えるとき,
これを集合(set)という.
その範囲内の個々の対象物を元
または要素(element)という.
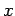 が集合
が集合 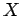 の元であることを,
の元であることを,
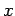 は
は 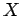 に属する(belong),
または
に属する(belong),
または 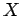 は
は 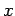 を含む(包含する)(contain)といい,
を含む(包含する)(contain)といい,
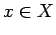 と表記する.その否定を
と表記する.その否定を 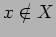 と表記する.
と表記する.
と表記する.
ある元 ![]() が条件
が条件 ![]() をみたすとする.
このとき,条件をみたす
をみたすとする.
このとき,条件をみたす ![]() 全体の集合を
全体の集合を
と表記する.
定義 1.2 (数の集合)
- 自然数(natural number)全体の集合:
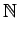
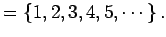
- 整数(integer)全体の集合:
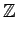
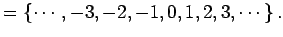
- 有理数(rational number, rational integer)全体の集合:
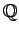
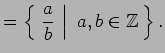
- 実数(real number)全体の集合:
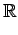
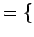 有理数と無理数(irrational number)全体の集合
有理数と無理数(irrational number)全体の集合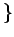
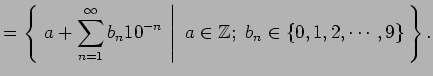
- 複素数(complex number)全体の集合:
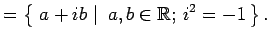
定義 1.3 (行列の集合)
- 実列ベクトル全体の集合:
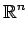
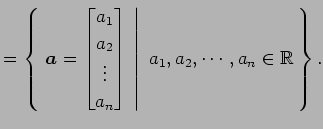
- 複素列ベクトル全体の集合:
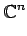
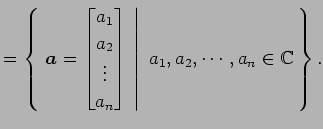
- 実行ベクトル全体の集合:
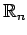
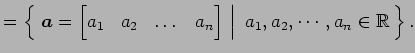
- 複素行ベクトル全体の集合:
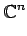
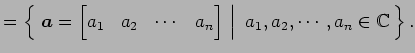
- 実行列全体の集合:
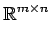
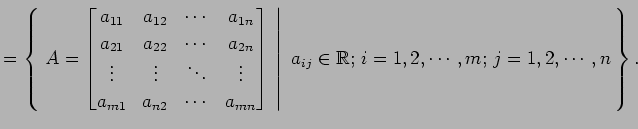
- 複素行列全体の集合:
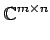
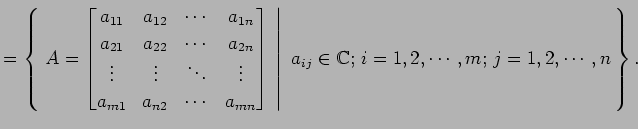
定義 1.4 (その他の集合)
- 高々
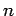 次の実係数多項式全体の集合:
次の実係数多項式全体の集合:
![$\displaystyle \mathbb{R}[x]_{n}$](img31.png)
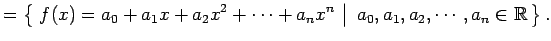
- 区間
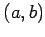 で連続な関数全体の集合:
で連続な関数全体の集合: 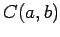 .
.
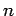 回微分可能でかつ
回微分可能でかつ 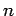 階導関数が連続な関数全体の集合:
階導関数が連続な関数全体の集合: 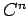 .
.
- 無限回微分可能な関数全体の集合:
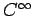 .
.
Kondo Koichi

平成18年1月17日