2.11 基本ベクトル
定義 2.41 (基本ベクトル)
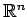 のベクトル
のベクトル
を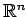 の
基本ベクトル(elemental vector)という.
の
基本ベクトル(elemental vector)という.
 |
を
注意 2.42 (基本ベクトルのノルム)
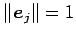
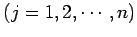 であるから,
基本ベクトルはすべてノルムは
であるから,
基本ベクトルはすべてノルムは 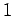 である.
である.
注意 2.43 (基本ベクトルの直交性)
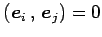
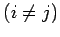 であるから,
異なる基本ベクトルどうしは直交する.
であるから,
異なる基本ベクトルどうしは直交する.
定理 2.44 (基本ベクトルと任意のベクトル)
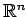 の任意のベクトル
の任意のベクトル
は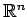 の基本ベトクル
の基本ベトクル
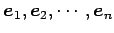 を
用いて
を
用いて
と表される.
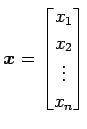 |
は
と表される.
Kondo Koichi

平成18年1月17日