2.7 ノルムの性質
定理 2.24 (ノルムの性質)
シュバルツの不等式(Schwartz' inequality):
が成り立つ.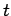 の 2 次式は
の 2 次式は
をみたさなければならない. よって
を得る.
(証明)
![]() ,
,
![]() に対して
に対して
| 0 | ||
が成り立つ.
をみたさなければならない. よって
を得る.
定理 2.25 (ノルムの性質)
三角不等式:
より
を得る.
(証明)
より
を得る.
定義 2.26 (ノルム)
ノルムはシュバルツの不等式と三角不等式をみたすものであればよい.
次に定義される式もノルムとなる.
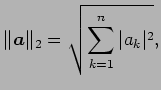 |
![$\displaystyle \Vert\vec{a}\Vert _{3}=\sqrt[3]{\sum_{k=1}^{n}\vert a_{k}\vert^3},$](img309.png) |
|||||
![$\displaystyle \Vert\vec{a}\Vert _{p}=\sqrt[p]{\sum_{k=1}^{n}\vert a_{k}\vert^p},$](img311.png) |
Kondo Koichi

平成18年1月17日