6.1 2 次曲線
![]() 内の曲線
内の曲線 ![]() を考える.
1 次式
を考える.
1 次式
で与えられる曲線は直線である. 2 次式
で与えられる曲線を2 次曲線という.
例 6.1 (放物線の例)
放物線は 2 次曲線である.
これを放物形という.
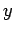 軸に対称な放物線
軸に対称な放物線 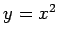 は
は 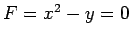 と
表されるので 2 次曲線である.
と
表されるので 2 次曲線である.
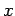 軸に対称な放物線
軸に対称な放物線 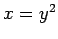 は
は 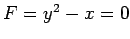 と
表されるので 2 次曲線である.
と
表されるので 2 次曲線である.
- 2 次曲線
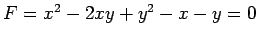 で与えられる曲線は
直線
で与えられる曲線は
直線 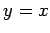 に対称な放物線である.
この放物線は曲線
に対称な放物線である.
この放物線は曲線 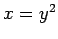 を
を 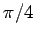 回転させたものであるから,
回転させたものであるから,
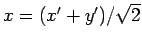 ,
,
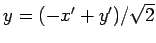 とし
とし 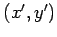 を
を 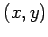 に置き換えれば
導出される.
に置き換えれば
導出される.
例 6.2 (楕円の例)
楕円は 2 次曲線である.
これを楕円形という.
- 楕円
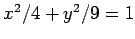 は
は
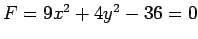 と
表されるので 2 次曲線である.
と
表されるので 2 次曲線である.
- 楕円
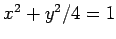 は
は
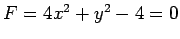 と
表されるので 2 次曲線である.
と
表されるので 2 次曲線である.
- 2 次曲線
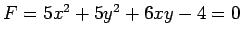 で与えられる曲線は楕円である.
この楕円は楕円
で与えられる曲線は楕円である.
この楕円は楕円
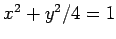 を
を 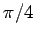 回転させたものと等しい.
回転させたものと等しい.
例 6.3 (双曲線の例)
双曲線は 2 次曲線である.
これを双曲形という.
- 双曲線
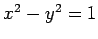 は
は
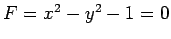 と
表されるので 2 次曲線である.
と
表されるので 2 次曲線である.
- 双曲線
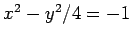 は
は
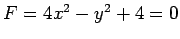 と
表されるので 2 次曲線である.
と
表されるので 2 次曲線である.
- 2 次曲線
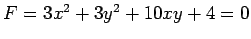 で与えられる曲線は双曲線である.
この双曲線は双曲線
で与えられる曲線は双曲線である.
この双曲線は双曲線
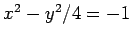 を
を 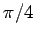 回転させたものと等しい.
回転させたものと等しい.
Kondo Koichi

平成18年1月17日