5.3 固有空間
注意 5.5 (固有ベクトルの定数倍の任意性)
線形変換  の固有値を
の固有値を 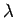 とし,
固有値
とし,
固有値 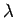 に属する固有ベクトルを
に属する固有ベクトルを 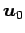 とする.
つまり
とする.
つまり
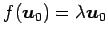 が成り立つ.
このとき,
が成り立つ.
このとき,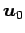 の定数
の定数
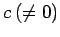 倍の
ベクトル
倍の
ベクトル
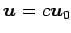 を考える.
ベクトル
を考える.
ベクトル 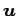 もまた
もまた 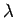 に属する
に属する  の固有ベクトル
となる.
なぜなら,
の固有ベクトル
となる.
なぜなら,
が成り立つからである. これより固有ベクトルには定数倍に任意性がある.
が成り立つからである. これより固有ベクトルには定数倍に任意性がある.
定義 5.6 (固有空間)
ベクトル空間 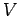 における線形変換
における線形変換 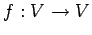 の
固有値を
の
固有値を 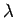 とする.
このとき
とする.
このとき
を の固有値
の固有値 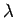 の固有空間(eigenspace)という.
の固有空間(eigenspace)という.
を
注意 5.7 (固有空間)
固有ベクトルは 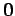 を除外しているが,
固有空間では
を除外しているが,
固有空間では 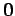 を含むことに注意する.
を含むことに注意する.
定理 5.8 (固有空間は部分空間)
固有空間
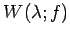 は
は 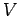 の部分空間である.
の部分空間である.
が成り立つので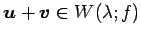 となる.
(iii)
となる.
(iii)
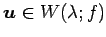 のとき
のとき
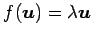 が成り立つ.
このとき
が成り立つ.
このとき 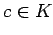 に対して
に対して
が成り立つので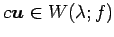 となる.
以上より(i), (ii), (iii)が成り立つので
となる.
以上より(i), (ii), (iii)が成り立つので
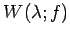 は
は 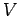 の
部分空間である.
の
部分空間である.
(証明)
(i)
![]() より
より
![]() となる.
(ii)
となる.
(ii)
![]() のとき
のとき
![]() ,
,
![]() が成り立つ.
このとき
が成り立つ.
このとき ![]() ,
, ![]() に対して
に対して
が成り立つので
が成り立つので
Kondo Koichi

平成18年1月17日