1.8 合成写像

定義 1.30 (合成写像)   写像 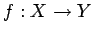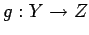$f:X\to Y$, $g:Y\to Z$ に対して，

$$h: X\to Z; \qquad z=h(x)=g(f(x))$$

で定義される写像を

$$h=g\circ f$$

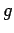と表記し，$f$ と $g$ の合成写像（composite）という．

例 1.31 (合成写像の具体例)   写像

$$f:\mathbb{R}\to\mathbb{R};\qquad y=f(x)=2x+1,$$

$$g:\mathbb{R}\to\mathbb{R};\qquad z=g(y)=y^2-1$$

の合成写像は

$$h=g\circ f:\mathbb{R}\to\mathbb{R};$$

$$z=h(x)=(g\circ f)(x)=g(f(x))=g(2x+1)=(2x+1)^2-1=4x(x+1)$$

である．

定理 1.32 (合成写像の性質)   写像の合成に対して結合則

$$(h\circ g)\circ f= h\circ (g\circ f)$$

が成り立つ．

Kondo Koichi
平成18年1月17日