4.12 余因子展開
定理 4.74 (余因子展開)
行列式  に対して
に対して
が成り立つ. これを第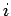 行に関する余因子展開という.
また,
行に関する余因子展開という.
また,
が成り立つ. これを第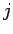 列に関する余因子展開という.
列に関する余因子展開という.
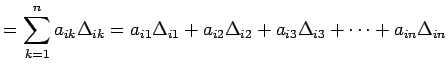 |
(756) | |
| (757) | ||
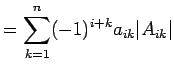 |
(758) |
が成り立つ. これを第
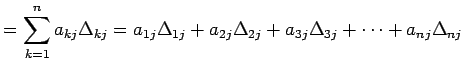 |
(759) | |
| (760) | ||
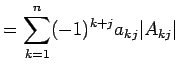 |
(761) |
が成り立つ. これを第
問 4.75 (余因子展開)
これを示せ.
となる. 次に第一行目の行ベクトルを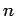 個のベクトルとしてみなし,
行列式を
個のベクトルとしてみなし,
行列式を 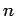 個に分解すると
個に分解すると
となる. 各項の第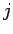 列を第一列に移動すると
列を第一列に移動すると
となる.各項を第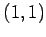 成分で展開すると
成分で展開すると
を得る. 同様の操作で列に関する余因子展開は示される.
(証明)
第 ![]() 行に関する余因子展開を示す.
まず行列式
行に関する余因子展開を示す.
まず行列式 ![]() の第
の第 ![]() 行目を第一行目に移動すると
行目を第一行目に移動すると
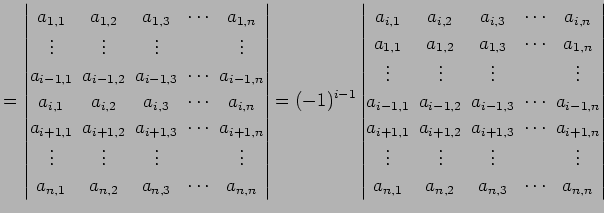 |
(762) |
となる. 次に第一行目の行ベクトルを
| (763) | ||
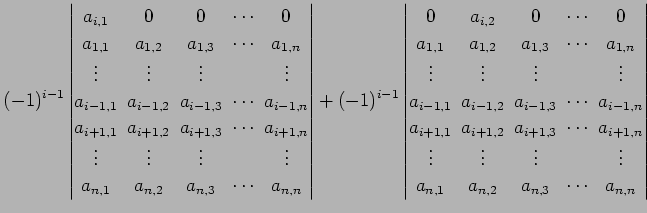 |
(764) | |
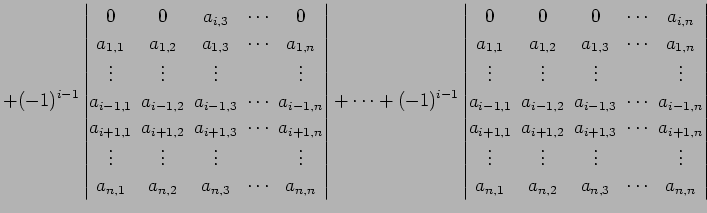 |
(765) |
となる. 各項の第
| (766) | ||
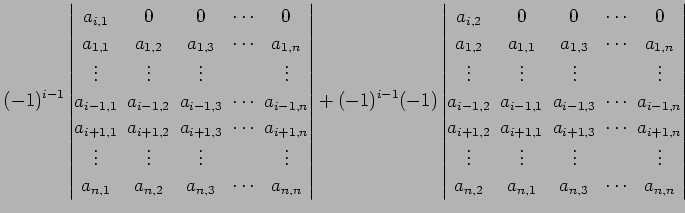 |
(767) | |
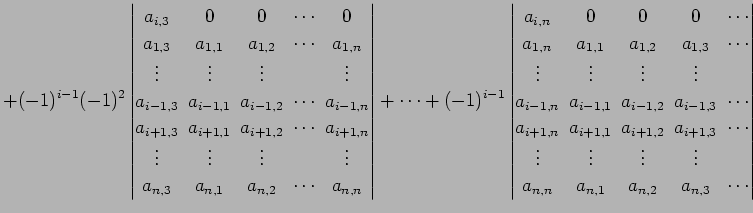 |
(768) |
となる.各項を第
| (769) | ||
| (770) | ||
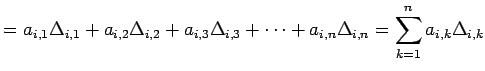 |
(771) |
を得る. 同様の操作で列に関する余因子展開は示される.
例 4.76 (余因子展開の計算例)
第 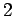 列目で余因子展開し,
列目で余因子展開し,
を得る.
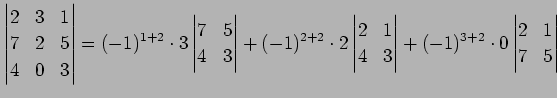 |
(772) | |
| (773) |
を得る.
例 4.77 (余因子展開の計算例)
第 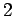 行目で余因子展開し,
行目で余因子展開し,
を得る.
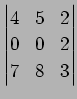 |
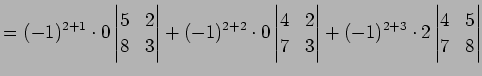 |
(774) |
| (775) |
を得る.
例 4.78 (余因子展開の計算例)
第一行目を余因子展開し,
を得る.
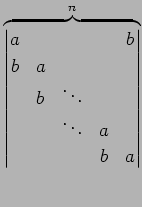 |
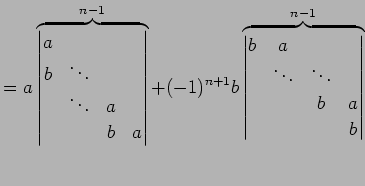 |
(776) |
| (777) |
を得る.
Kondo Koichi

平成17年9月15日