3.2 ベクトルの 1 次結合と連立 1 次方程式
定義 3.4 (ベクトルの 1 次結合)
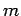 個のベクトル
個のベクトル
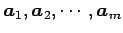 が
与えられたとき,ベクトル
が
与えられたとき,ベクトル
を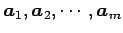 の
1 次結合(linear combination)と呼ぶ.
の
1 次結合(linear combination)と呼ぶ.
| (388) |
を
例 3.5 (ベクトルの 1 次結合の具体例)
2次の列ベクトル
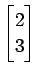 を
を
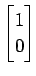 と
と
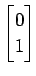 の
1 次結合で表すと
の
1 次結合で表すと
となる.
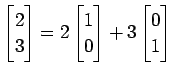 |
(389) |
となる.
連立 1 次方程式
![]() の
係数行列
の
係数行列 ![]() を
列ベクトルで分割し
を
列ベクトルで分割し
![]() と書き直すと,
方程式は
と書き直すと,
方程式は
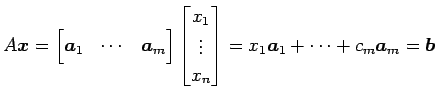 |
(390) |
となる. すなわち
例 3.6 (ベクトルの 1 次結合と連立 1 次方程式の関係の具体例)
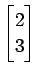 を
を
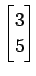 と
と
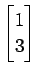 の 1 次結合で表す.
すなわち
の 1 次結合で表す.
すなわち
を満たす係数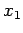 ,
, 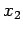 を求める.
これを書き直すと
を求める.
これを書き直すと
となる. 結局,連立 1 次方程式を求める問題に帰着する. これを解くと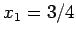 ,
,
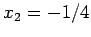 となる.
よって
となる.
よって
を得る.
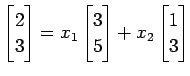 |
(391) |
を満たす係数
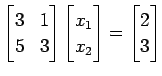 |
(392) |
となる. 結局,連立 1 次方程式を求める問題に帰着する. これを解くと
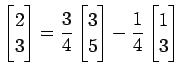 |
(393) |
を得る.
問 3.7
教科書(p.18) 問題1.4 3.-6.
Kondo Koichi

平成17年9月15日