2.14 行列の演算に関する緒性質
定理 2.53 (行列の演算の性質)
行列の演算に関して次の性質が成り立つ:
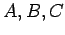 の型は互いに演算が定義されている型とする.
の型は互いに演算が定義されている型とする.
- (1)
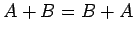 (加法の交換則)
(加法の交換則)
- (2)
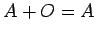 ,
, 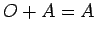 (加法の零元)
(加法の零元) 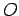 は数の足し算の 0 と同様な振る舞い
は数の足し算の 0 と同様な振る舞い
- (3)
-
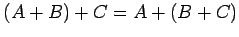 (加法の結合則)
(加法の結合則)
- (4)
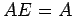 ,
, 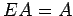 (乗法の単位元)
(乗法の単位元) 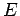 は数の掛け算の
は数の掛け算の 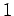 と同様な振る舞い
と同様な振る舞い
- (5)
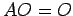 ,
, 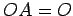 (乗法の零元)
(乗法の零元) 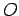 は数の掛け算の 0 と同様な振る舞い
は数の掛け算の 0 と同様な振る舞い
- (6)
-
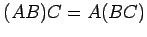 (乗法の結合則)
(乗法の結合則)
- (7)
-
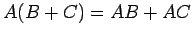 ,
,
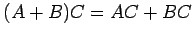 (分配則)
(分配則)
- (8)
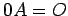 ,
, 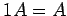
- (9)
-
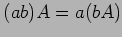 ,
,
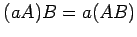
- (10)
-
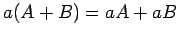 ,
,
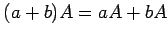
- (11)
-
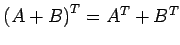
- (12)
-
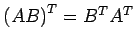
- (13)
-
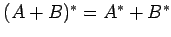
- (14)
-
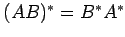
- (15)
-
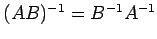
問 2.54 (行列の演算の性質)
となる.次に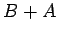 を求める.和の定義より
を求める.和の定義より
となる.各要素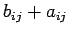 は単に数なので,
和について可換である.
よってすべての要素の和の順番を入れ換えて,
は単に数なので,
和について可換である.
よってすべての要素の和の順番を入れ換えて,
となる.以上より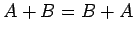 が示された.
が示された.
を得る.これより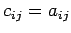 が成り立つ.
よって
が成り立つ.
よって 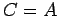 を得る.
以上より
を得る.
以上より 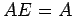 が示された.
が示された.
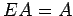 の場合も同様に示す.
の場合も同様に示す.
となる.転置の操作は行と列を入れ換えるので
となる.右辺の行列を二つの行列の和に分解し, それぞれの行列の転置をとると
を得る. 以上で示された.
とおく. 次に
とおく. まず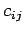 ,
, 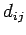 を求める.
積の定義より
を求める.
積の定義より
となる.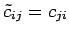 ,
,
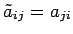 ,
,
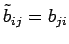 を用いれば
を用いれば
を得る.以上より![$ {(AB)}^{T}={C}^{T}=[\tilde{c}_{ij}]_{r\times m}=
[d_{ij}]_{r\times n}=D={B}^{T}{A}^{T}$](img739.png) となる.
証明終了.
となる.
証明終了.
性質(1)-(12)を示せ.
(証明)(1), (4), (11), (12) を示す.残りは自習.
(1) ![]() を示す.まず
を示す.まず
![]() ,
,
![]() とおく.
このとき
とおく.
このとき ![]() は和の定義より
は和の定義より
| (306) |
となる.次に
| (307) |
となる.各要素
| (308) |
となる.以上より
(4) ![]() を示す.まず
を示す.まず
![]() ,
,
![]() とおく.
さらに
とおく.
さらに
![]() とおく.
とおく.
![]() を計算する.
積の定義とクロネッカーのデルタの定義に従って計算する.
を計算する.
積の定義とクロネッカーのデルタの定義に従って計算する.
![]() より
より
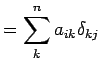 |
(309) | |
| (310) | ||
| (311) | ||
| (312) |
を得る.これより
(11)
![]() を示す.
まず,
を示す.
まず,
![]() ,
,
![]() とおく.
和の定義より
とおく.
和の定義より
| (313) |
となる.転置の操作は行と列を入れ換えるので
| (314) |
となる.右辺の行列を二つの行列の和に分解し, それぞれの行列の転置をとると
| (315) |
を得る. 以上で示された.
(12)
![]() を示す.まず
を示す.まず
| (316) |
とおく. 次に
| (317) |
とおく. まず
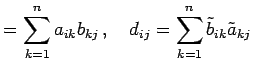 |
(318) |
となる.
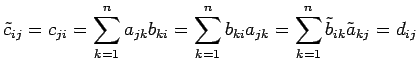 |
(319) |
を得る.以上より
Kondo Koichi

平成17年9月15日